第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
7. 如图,将边长为 $20$ cm 的正方形纸片的四个角各剪去一个边长为 $x$ cm 的小正方形.
(1)求阴影部分的面积 $S$(用含 $x$ 的式子表示);
(2)当 $x = 3$ 时,求阴影部分的面积 $S$.

(1)求阴影部分的面积 $S$(用含 $x$ 的式子表示);
(2)当 $x = 3$ 时,求阴影部分的面积 $S$.

答案:
(1)
原正方形边长为$20cm$,根据正方形面积公式$S = a^2$($a$为边长),原正方形面积为$20×20 = 400cm^2$。
四个角都剪去一个边长为$xcm$的小正方形,每个小正方形面积为$x× x=x^{2}cm^{2}$,四个小正方形面积为$4x^{2}cm^{2}$。
则阴影部分面积$S = 400 - 4x^{2}$。
(2)
当$x = 3$时,把$x = 3$代入$S = 400 - 4x^{2}$中,
$S=400-4×3^{2}$
$=400 - 4×9$
$=400 - 36$
$= 364cm^{2}$
答:
(1)$S = 400 - 4x^{2}$;
(2)当$x = 3$时,阴影部分面积$S$为$364cm^{2}$。
(1)
原正方形边长为$20cm$,根据正方形面积公式$S = a^2$($a$为边长),原正方形面积为$20×20 = 400cm^2$。
四个角都剪去一个边长为$xcm$的小正方形,每个小正方形面积为$x× x=x^{2}cm^{2}$,四个小正方形面积为$4x^{2}cm^{2}$。
则阴影部分面积$S = 400 - 4x^{2}$。
(2)
当$x = 3$时,把$x = 3$代入$S = 400 - 4x^{2}$中,
$S=400-4×3^{2}$
$=400 - 4×9$
$=400 - 36$
$= 364cm^{2}$
答:
(1)$S = 400 - 4x^{2}$;
(2)当$x = 3$时,阴影部分面积$S$为$364cm^{2}$。
8. 用圆圈按图示的规律拼图案,其中第 $1$ 个图案中有 $2$ 个圆圈,第 $2$ 个图案中有 $5$ 个圆圈,第 $3$ 个图案中有 $8$ 个圆圈,第 $4$ 个图案中有 $11$ 个圆圈……按此规律排列下去,则第 $7$ 个图案中圆圈的个数为(
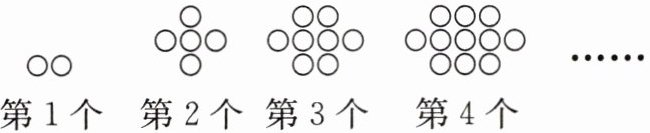
A.$14$
B.$20$
C.$23$
D.$26$
B
)
A.$14$
B.$20$
C.$23$
D.$26$
答案:
B
9. 观察下面这一列数:$1$,$-2$,$3$,$-4$,$5$,$-6$,$7$,$-8$,…$$.
(1)当 $n > 1$ 时,这列数的第 $n$ 个数是多少(用含 $n$ 的式子表示)?
(2)这列数的第 $100$ 个数是多少?
(3)$2025$ 是不是这列数中的数?如果是,是第几个数?
(1)当 $n > 1$ 时,这列数的第 $n$ 个数是多少(用含 $n$ 的式子表示)?
(2)这列数的第 $100$ 个数是多少?
(3)$2025$ 是不是这列数中的数?如果是,是第几个数?
答案:
(1) 观察这列数,奇数项为正,偶数项为负,绝对值等于项数。所以第$n$个数是$(-1)^{n+1}n$。
(2) 当$n = 100$时,$(-1)^{100+1}×100 = (-1)^{101}×100=-100$。
(3) 假设$2025$是这列数中的数,令$(-1)^{n+1}n = 2025$。因为$2025$是正数,所以$(-1)^{n+1}=1$,则$n+1$为偶数,$n$为奇数,此时$n = 2025$。所以$2025$是这列数中的数,是第$2025$个数。
(1)$(-1)^{n+1}n$
(2)$-100$
(3)是,第$2025$个数
(1) 观察这列数,奇数项为正,偶数项为负,绝对值等于项数。所以第$n$个数是$(-1)^{n+1}n$。
(2) 当$n = 100$时,$(-1)^{100+1}×100 = (-1)^{101}×100=-100$。
(3) 假设$2025$是这列数中的数,令$(-1)^{n+1}n = 2025$。因为$2025$是正数,所以$(-1)^{n+1}=1$,则$n+1$为偶数,$n$为奇数,此时$n = 2025$。所以$2025$是这列数中的数,是第$2025$个数。
(1)$(-1)^{n+1}n$
(2)$-100$
(3)是,第$2025$个数
查看更多完整答案,请扫码查看


