第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 下列计算不正确的是(
A.$9×6 = 54$
B.$(-9)×6 = -54$
C.$3×(-4) = 12$
D.$(-3)×(-4) = 12$
C
)A.$9×6 = 54$
B.$(-9)×6 = -54$
C.$3×(-4) = 12$
D.$(-3)×(-4) = 12$
答案:
C
2. 下列说法错误的是(
A.一个数与 $1$ 相乘,仍得原数
B.一个数与 $0$ 相乘,得 $0$
C.互为倒数的两个数的积是 $0$
D.一个数与 $-1$ 相乘,得原数的相反数
C
)A.一个数与 $1$ 相乘,仍得原数
B.一个数与 $0$ 相乘,得 $0$
C.互为倒数的两个数的积是 $0$
D.一个数与 $-1$ 相乘,得原数的相反数
答案:
C
3. 如图,数轴上的三点 $A$,$B$,$C$ 所表示的数分别为 $a$,$b$,$c$,下列各式正确的是(
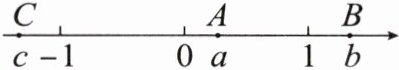
A.$(a - 1)(b - 1) > 0$
B.$(b - 1)(c - 1) > 0$
C.$(a + 1)(b + 1) < 0$
D.$(b + 1)(c + 1) < 0$
D
)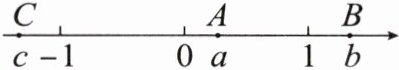
A.$(a - 1)(b - 1) > 0$
B.$(b - 1)(c - 1) > 0$
C.$(a + 1)(b + 1) < 0$
D.$(b + 1)(c + 1) < 0$
答案:
D
4. 已知 $x = -2$,$y = 4$,则 $|xy| = $
8
。
答案:
$8$(这里按照要求只需填写数值结果对应的空白处内容,若题目是填空形式,答案就写该空应填的值)
5. 如果 $□×(-\frac{1}{6}) = 1$,那么 $□$ 中应填的数是
-6
。
答案:
-6
6. $(-7)×4$ 的倒数是
$-\frac{1}{28}$
。
答案:
$-\frac{1}{28}$
7. $a$,$b$ 互为相反数,$c$,$d$ 互为倒数,则 $2(a + b) + cd = $
1
。
答案:
1
8. 计算:
(1) $(-\frac{1018}{1019})×0$;
(2) $(-\frac{6}{5})×(-\frac{15}{6})$;
(3) $(-26)×(+\frac{7}{13})$;
(4) $(-0.8)×(-\frac{7}{4})$。
(1) $(-\frac{1018}{1019})×0$;
(2) $(-\frac{6}{5})×(-\frac{15}{6})$;
(3) $(-26)×(+\frac{7}{13})$;
(4) $(-0.8)×(-\frac{7}{4})$。
答案:
(1)
根据任何数与 0 相乘都等于 0,可得:
$(-\frac{1018}{1019})×0 = 0$
(2)
根据有理数乘法法则:两数相乘,同号得正,并把绝对值相乘,可得:
$(-\frac{6}{5})×(-\frac{15}{6})=\frac{6}{5}×\frac{15}{6}= 3$
(3)
根据有理数乘法法则:两数相乘,异号得负,并把绝对值相乘,可得:
$(-26)×(+\frac{7}{13})=-(26×\frac{7}{13})=-14$
(4)
先将$-0.8$化为分数$-\frac{4}{5}$,再根据有理数乘法法则:两数相乘,同号得正,并把绝对值相乘,可得:
$(-0.8)×(-\frac{7}{4})=(-\frac{4}{5})×(-\frac{7}{4})=\frac{4}{5}×\frac{7}{4}=\frac{7}{5}=1.4$
(1)
根据任何数与 0 相乘都等于 0,可得:
$(-\frac{1018}{1019})×0 = 0$
(2)
根据有理数乘法法则:两数相乘,同号得正,并把绝对值相乘,可得:
$(-\frac{6}{5})×(-\frac{15}{6})=\frac{6}{5}×\frac{15}{6}= 3$
(3)
根据有理数乘法法则:两数相乘,异号得负,并把绝对值相乘,可得:
$(-26)×(+\frac{7}{13})=-(26×\frac{7}{13})=-14$
(4)
先将$-0.8$化为分数$-\frac{4}{5}$,再根据有理数乘法法则:两数相乘,同号得正,并把绝对值相乘,可得:
$(-0.8)×(-\frac{7}{4})=(-\frac{4}{5})×(-\frac{7}{4})=\frac{4}{5}×\frac{7}{4}=\frac{7}{5}=1.4$
9. 若 $|a| = 7$,$|b| = 3$。
(1) 若 $ab > 0$,求 $a + b$ 的值;
(2) 若 $|a + b| = a + b$,求 $ab$ 的值。
(1) 若 $ab > 0$,求 $a + b$ 的值;
(2) 若 $|a + b| = a + b$,求 $ab$ 的值。
答案:
(1)
∵|a|=7,
∴a=±7;
∵|b|=3,
∴b=±3。
∵ab>0,
∴a,b同号。
当a=7,b=3时,a+b=7+3=10;
当a=-7,b=-3时,a+b=-7+(-3)=-10。
∴a+b的值为10或-10。
(2)
∵|a+b|=a+b,
∴a+b≥0。
∵|a|=7,|b|=3,
∴a=±7,b=±3。
可能情况:
当a=7,b=3时,a+b=10≥0,ab=7×3=21;
当a=7,b=-3时,a+b=4≥0,ab=7×(-3)=-21;
当a=-7,b=3时,a+b=-4<0(舍去);
当a=-7,b=-3时,a+b=-10<0(舍去)。
∴ab的值为21或-21。
(1)
∵|a|=7,
∴a=±7;
∵|b|=3,
∴b=±3。
∵ab>0,
∴a,b同号。
当a=7,b=3时,a+b=7+3=10;
当a=-7,b=-3时,a+b=-7+(-3)=-10。
∴a+b的值为10或-10。
(2)
∵|a+b|=a+b,
∴a+b≥0。
∵|a|=7,|b|=3,
∴a=±7,b=±3。
可能情况:
当a=7,b=3时,a+b=10≥0,ab=7×3=21;
当a=7,b=-3时,a+b=4≥0,ab=7×(-3)=-21;
当a=-7,b=3时,a+b=-4<0(舍去);
当a=-7,b=-3时,a+b=-10<0(舍去)。
∴ab的值为21或-21。
10. 观察下列式子,填空:
(1) $(-11)×99 = -1089$;
(2) $(-111)×999 = -110889$;
(3) $(-1111)×9999 = $
(4) $(-\underbrace{11…1}_{2024个1})×\underbrace{99…9}_{2024个9} = $
(1) $(-11)×99 = -1089$;
(2) $(-111)×999 = -110889$;
(3) $(-1111)×9999 = $
$-11108889$
;(4) $(-\underbrace{11…1}_{2024个1})×\underbrace{99…9}_{2024个9} = $
$-\underbrace{11\cdots1}_{2023个1}0\underbrace{88\cdots8}_{2023个8}9$
。
答案:
(3)$-11108889$;
(4)$-\underbrace{11\cdots1}_{2023个1}0\underbrace{88\cdots8}_{2023个8}9$
(3)$-11108889$;
(4)$-\underbrace{11\cdots1}_{2023个1}0\underbrace{88\cdots8}_{2023个8}9$
查看更多完整答案,请扫码查看


