第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
20.下面是圆圆解方程$\frac{x + 1}{2} - \frac{x - 3}{3} = 1$的过程.
解:去分母,得$3(x + 1) - 2(x - 3) = 1$.
去括号,得$3x + 1 - 2x + 3 = 1$.
移项、合并同类项,得$x = -3$.
圆圆解方程的过程是否有错误?如果有错误,请指出来,并写出正确的解方程的过程.
解:去分母,得$3(x + 1) - 2(x - 3) = 1$.
去括号,得$3x + 1 - 2x + 3 = 1$.
移项、合并同类项,得$x = -3$.
圆圆解方程的过程是否有错误?如果有错误,请指出来,并写出正确的解方程的过程.
答案:
圆圆的解法有错误。
错误之处:
1. 去分母时,等式右边的1未乘6,应为6;
2. 去括号时,3(x+1)展开后应为3x+3,-2(x-3)展开后应为-2x+6。
正确过程:
去分母,得$3(x + 1) - 2(x - 3) = 6$
去括号,得$3x + 3 - 2x + 6 = 6$
移项,得$3x - 2x = 6 - 3 - 6$
合并同类项,得$x = -3$
结论:方程的解为$x = -3$
错误之处:
1. 去分母时,等式右边的1未乘6,应为6;
2. 去括号时,3(x+1)展开后应为3x+3,-2(x-3)展开后应为-2x+6。
正确过程:
去分母,得$3(x + 1) - 2(x - 3) = 6$
去括号,得$3x + 3 - 2x + 6 = 6$
移项,得$3x - 2x = 6 - 3 - 6$
合并同类项,得$x = -3$
结论:方程的解为$x = -3$
21.已知关于$x的方程x - 2m = -3x + 4与2 - m = x$的解互为相反数.
(1)求$m$的值;
(2)求这两个方程的解.
(1)求$m$的值;
(2)求这两个方程的解.
答案:
(1)解方程$x - 2m = -3x + 4$:
移项得$x + 3x = 4 + 2m$,
合并同类项得$4x = 4 + 2m$,
系数化为1得$x = \frac{2 + m}{2}$。
解方程$2 - m = x$得$x = 2 - m$。
由两解互为相反数,得$\frac{2 + m}{2} + (2 - m) = 0$,
去分母得$2 + m + 4 - 2m = 0$,
合并同类项得$6 - m = 0$,
解得$m = 6$。
(2)当$m = 6$时,
第一个方程的解为$x = \frac{2 + 6}{2} = 4$,
第二个方程的解为$x = 2 - 6 = -4$。
(1)解方程$x - 2m = -3x + 4$:
移项得$x + 3x = 4 + 2m$,
合并同类项得$4x = 4 + 2m$,
系数化为1得$x = \frac{2 + m}{2}$。
解方程$2 - m = x$得$x = 2 - m$。
由两解互为相反数,得$\frac{2 + m}{2} + (2 - m) = 0$,
去分母得$2 + m + 4 - 2m = 0$,
合并同类项得$6 - m = 0$,
解得$m = 6$。
(2)当$m = 6$时,
第一个方程的解为$x = \frac{2 + 6}{2} = 4$,
第二个方程的解为$x = 2 - 6 = -4$。
22.小明在解关于$x的方程\frac{3x - 2}{5} = \frac{x - a}{10} - 2$的过程中,去分母时,方程右边的一2没有乘10,因而得到错误的解为$x = -\frac{1}{5}$,求出方程的正确解.
答案:
1. 首先根据错误的去分母方法得到方程:
小明去分母时方程右边的$-2$没有乘$10$,原方程$\frac{3x - 2}{5}=\frac{x - a}{10}-2$去分母(错误操作)得$2(3x - 2)=x - a-2$。
展开式子:$6x-4 = x - a-2$。
移项可得:$6x - x=-a - 2 + 4$,即$5x=-a + 2$,解得$x=\frac{-a + 2}{5}$。
已知错误解$x =-\frac{1}{5}$,所以$\frac{-a + 2}{5}=-\frac{1}{5}$。
两边同时乘以$5$得:$-a + 2=-1$,移项可得$a = 3$。
2. 然后将$a = 3$代入原方程求解:
原方程为$\frac{3x - 2}{5}=\frac{x - 3}{10}-2$。
去分母(两边同时乘以$10$):$10×\frac{3x - 2}{5}=10×\frac{x - 3}{10}-10×2$,即$2(3x - 2)=x - 3-20$。
展开式子:$6x-4=x - 23$。
移项:$6x - x=-23 + 4$。
合并同类项:$5x=-19$。
系数化为$1$:$x=-\frac{19}{5}$。
所以,原方程的正确解为$x =-\frac{19}{5}$。
小明去分母时方程右边的$-2$没有乘$10$,原方程$\frac{3x - 2}{5}=\frac{x - a}{10}-2$去分母(错误操作)得$2(3x - 2)=x - a-2$。
展开式子:$6x-4 = x - a-2$。
移项可得:$6x - x=-a - 2 + 4$,即$5x=-a + 2$,解得$x=\frac{-a + 2}{5}$。
已知错误解$x =-\frac{1}{5}$,所以$\frac{-a + 2}{5}=-\frac{1}{5}$。
两边同时乘以$5$得:$-a + 2=-1$,移项可得$a = 3$。
2. 然后将$a = 3$代入原方程求解:
原方程为$\frac{3x - 2}{5}=\frac{x - 3}{10}-2$。
去分母(两边同时乘以$10$):$10×\frac{3x - 2}{5}=10×\frac{x - 3}{10}-10×2$,即$2(3x - 2)=x - 3-20$。
展开式子:$6x-4=x - 23$。
移项:$6x - x=-23 + 4$。
合并同类项:$5x=-19$。
系数化为$1$:$x=-\frac{19}{5}$。
所以,原方程的正确解为$x =-\frac{19}{5}$。
23.下面是嘉嘉和淇淇玩游戏时两人的对话.
嘉嘉:你心里随便想一个数,然后如图示的步骤正确操作,我就能立刻说出你想的那个数.
淇淇:真的吗?这么神奇!那我来试试.
想一个数$\to × 3 \to -6 \to ÷ 3 \to +7 \to$结果告诉嘉嘉
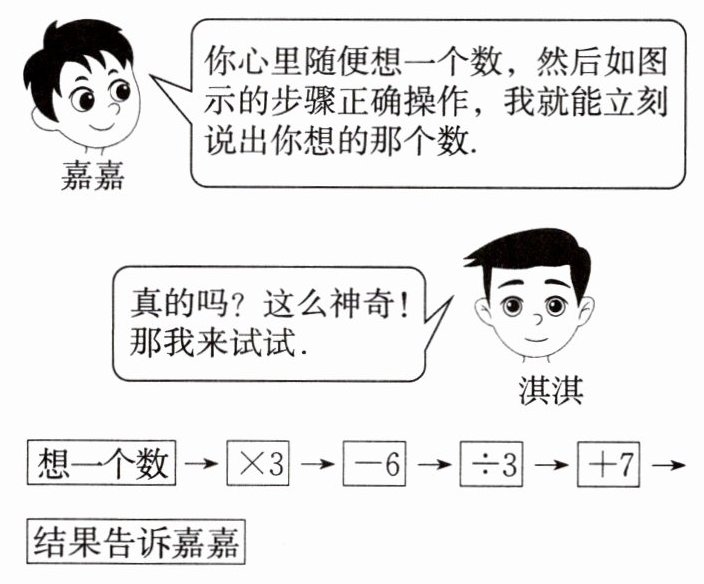
(1)如果淇淇想的数是$-5$,求淇淇告诉嘉嘉的结果.
(2)如果淇淇告诉嘉嘉的结果是21,求淇淇想的那个数.
嘉嘉:你心里随便想一个数,然后如图示的步骤正确操作,我就能立刻说出你想的那个数.
淇淇:真的吗?这么神奇!那我来试试.
想一个数$\to × 3 \to -6 \to ÷ 3 \to +7 \to$结果告诉嘉嘉

(1)如果淇淇想的数是$-5$,求淇淇告诉嘉嘉的结果.
(2)如果淇淇告诉嘉嘉的结果是21,求淇淇想的那个数.
答案:
(1)
若淇淇想的数是$-5$,
$-5×3=-15$;
$-15 - 6=-21$;
$-21÷3=-7$;
$-7 + 7 = 0$。
所以淇淇告诉嘉嘉的结果是$0$。
(2)
设淇淇想的数是$x$,
$\dfrac{3x - 6}{3}+7 = 21$,
$\dfrac{3x - 6}{3}=21 - 7$,
$\dfrac{3x - 6}{3}=14$,
$3x - 6 = 42$,
$3x=42 + 6$,
$3x=48$,
$x = 16$。
所以淇淇想的那个数是$16$。
(1)
若淇淇想的数是$-5$,
$-5×3=-15$;
$-15 - 6=-21$;
$-21÷3=-7$;
$-7 + 7 = 0$。
所以淇淇告诉嘉嘉的结果是$0$。
(2)
设淇淇想的数是$x$,
$\dfrac{3x - 6}{3}+7 = 21$,
$\dfrac{3x - 6}{3}=21 - 7$,
$\dfrac{3x - 6}{3}=14$,
$3x - 6 = 42$,
$3x=42 + 6$,
$3x=48$,
$x = 16$。
所以淇淇想的那个数是$16$。
查看更多完整答案,请扫码查看


