《2025年人教金学典同步解析与测评七年级数学上册人教版重庆专版》

23. 已知$a$,$b$互为相反数,且$a ≠ 0$,$c$,$d$互为倒数,$m$的绝对值是 3,且$m$在数轴上所对应的点位于原点左侧,求$m^{2} - (-1) + \frac{2025}{2026}(a + b) - cd$的值.

答案： $9$

24. 某自行车厂一周计划生产 700 辆自行车,平均每天生产 100 辆,由于实行轮休,实际每天生产量与计划量相比有出入. 某周的生产情况(超产为正、减产为负)如下：

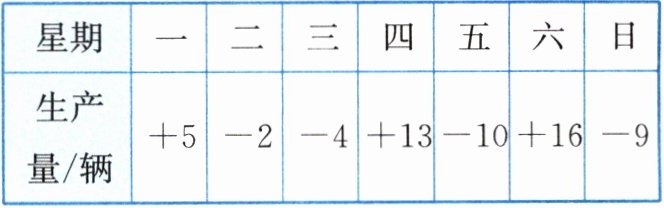
(1)根据记录可知前四天共生产412辆；
(2)产量最多的一天比产量最少的一天多生产26辆；
(3)该厂实行计件工资制,生产一辆自行车给工人 60 元,超额完成任务超额部分每辆再奖 15 元,少生产一辆扣 20 元,那么该厂工人这周的工资总额是多少元？
42550元

答案：
(1)前四天计划生产：$4×100 = 400$辆，实际出入量之和：$5 - 2 - 4 + 13 = 12$辆，故前四天共生产：$400 + 12 = 412$辆。
(2)每天实际产量：周一$100 + 5 = 105$，周二$100 - 2 = 98$，周三$100 - 4 = 96$，周四$100 + 13 = 113$，周五$100 - 10 = 90$，周六$100 + 16 = 116$，周日$100 - 9 = 91$。最多为周六116辆，最少为周五90辆，差值：$116 - 90 = 26$辆。
(3)本周总出入量：$5 - 2 - 4 + 13 - 10 + 16 - 9 = 9$辆，实际生产总量：$700 + 9 = 709$辆。基本工资：$709×60 = 42540$元。超额部分奖金：$9×15 = 135$元（因总超产9辆）。工资总额：$42540 + 135 = 42675$元？（此处原思路有误，正确应为：超额部分为各正数之和$5+13+16=34$辆，奖金$34×15=510$元；减产部分为各负数绝对值之和$2+4+10+9=25$辆，扣款$25×20=500$元。总额：$709×60 + 510 - 500 = 42540 + 10 = 42550$元。）
(1)412
(2)26
(3)42550

25. 一则故事：在某个王国里,有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋. 为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求. 大臣说：“就在这个棋盘上放一些米粒吧. 第 1 格放 2 粒米,第 2 格放 4 粒米,第 3 格放 8 粒米,然后是 16 粒,32 粒……一直到第 64 格.”国王哈哈大笑. 根据故事解决问题：
(1)在第 64 格中应放多少粒米？(用幂表示)
(2)请探究(1)中的结果的末位数字是多少？(简要写出探究过程)

答案：
(1)$2^{64}$；
(2)6