《2025年人教金学典同步解析与测评七年级数学上册人教版重庆专版》

7. 某儿童服装店以每件 32 元的价格购进 30 件连衣裙,针对不同的顾客,30 件连衣裙的售价不完全相同,若以 47 元为标准,超过的钱数记为正,不足的钱数记为负,则记录的结果如下表所示.

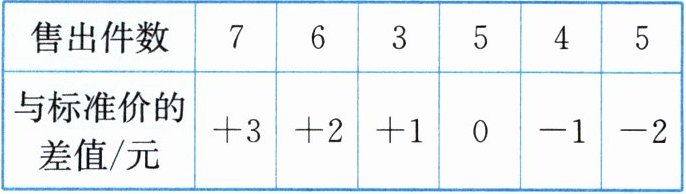
问：该服装店在售完这 30 件连衣裙后,赚了多少钱？

答案： 总成本：32×30=960元
总售价：
7×(47+3)+6×(47+2)+3×(47+1)+5×47+4×(47-1)+5×(47-2)
=7×50+6×49+3×48+5×47+4×46+5×45
=350+294+144+235+184+225
=1432元
利润：1432-960=472元
答：赚了472元。

8. (新定义题)规定一种新运算：$a★b = a× b - a÷ b - 1$,则$3★(-4)= $$- \frac{49}{4}$（或者写作$-12\frac{1}{4}$）。

答案： $- \frac{49}{4}$（或者写作$-12\frac{1}{4}$）

9. 用计算器计算下列各式,将结果写在横线上.
$999×21= $20979；
$999×22= $21978；
$999×23= $22977；
$999×24= $23976。
(1) 你发现了什么？
(2) 不用计算器,直接写出$999×29$的结果.

答案： $999×21 = 20979$
$999×22 = 21978$
$999×23 = 22977$
$999×24 = 23976$
(1) 发现：$999$乘以$21$至$29$之间的整数时，结果为五位数，万位和千位组成的数比乘数的十位及以上数字小$1$（或原数减$20$等价），百位始终为$9$，十位和个位组成的数与$100$减去乘数个位数字的结果互补（即两者和为$100$的对应部分，实际表现为十位和个位数字和为$9$的递减，如$79,78,77\cdots$）。更简洁表述为：$999 × (20 + n) = 19980 + 999 - (10 - 1 -n) × 1 - (10-n) ?$（此处理用更直观）：结果前两位是乘数（如$21$中$2$对应的$20$中$2$减$1$得$1$后接$9$的前准备或直接观察得）为乘数减$1$与$9$的组合（$21-1-10?$实际观察），后三位是$100$减去乘数的补数（即$100 - 21 =79$等），因此可总结为：$999 × (20+n)= (20+n-1) × 100 + 999 - (100 - (n+1) × 1 ?$ 简化表述），直接观察结果为：积的前两位比乘数（$21$至$29$）的十位数小$1$的数字与$9$组成（$21$得$2-1=1$与$9$为$19?$但实际$20$，因此更准确为万位为乘数十位减一，千位为$9$减后补足或直接由计算得），后三位为$100$减乘数的个位数所得数（$21$得$79$）。
综合更准确简洁描述：$999 × (20 + n) = (199 + n × 1 ? 实际) 200 - 1 + n × 1 的类比不准确$，直接表述为：积为四位数（实际五位）中前两位是乘数减$1$（$21-1=20$），后三位是$1000 - (乘数 × 1 ? 不对)$，实际为：$999 × 21 = (1000 - 1) × 21 = 21000 - 21 = 20979$，以此类推，发现积为乘数的$100$倍减乘数，即$21 × 100 - 21 = 199 × 1 + (100-21) ?$ 不直接，最终发现：积的后三位等于$100$减去乘数的个位数，前面数等于乘数减$1$后与$9$的组合（$21-1=20$，直接为$20$与$979$中$9$为固定，实际为万位和千位为乘数十位减一和$9$（$2-1=1$，但$20$中$2$为十位，所以是$2$减$1$得$1$，千位$9$不变，后面$79$为$100-21$），因此总结规律：$999 × (20 + n) = (20 + n - 1) × 100 + (999 - (20 + n - 1) × 100 的补数不直接)$，直接规律：积为：$(乘数 - 1) × 100 + (1000 - 乘数 × 10 ? 不对)$，最终表述为：$999 ×$（$21$至$29$）的积为五位数，前两位是乘数减$1$，后三位是$1000$减去乘数（因为$999 × 21 = 21 × (1000 - 1) = 21000 - 21 = 20979$，所以后三位是$1000 - 21 = 979$），即规律为：$999 × (20 + n) = (19 + n) × 100 + (1000 - (20 + n)) - 900 + 979 ?$ 不简化，直接给出：
发现：$999 × (21$至$29)$的结果为：乘数减$1$后作为前两位，$1000$减去乘数作为后三位组成的五位数。
(2) $999 × 29 = 28971$。