《2025年初中升高中衔接读本南京出版社数学》

1. 如图,分别过点$P_{i}(i,0)(i= 1,2,…,n)作x$轴的垂线,交$y= \frac{1}{2}x^{2}的图像于点A_{i}$,交直线$y= -\frac{1}{2}x于点B_{i}$,则$\frac{1}{A_{1}B_{1}}+\frac{1}{A_{2}B_{2}}+…+\frac{1}{A_{n}B_{n}}$的值为( )


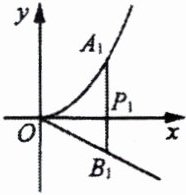
A.2
B.$\frac{2}{n+1}$
C.$\frac{2n}{n+1}$
D.$\frac{2}{n(n+1)}$

答案： C

2. 点$A,B的坐标分别为(-2,3)和(1,3)$,抛物线$y= ax^{2}+bx+c(a＜0)的顶点在线段AB$上运动时,形状保持不变,且与$x轴交于C,D$两点(点$C在点D$的左侧),给出下列结论:①$c＜3$;②当$x＜-3$时,$y随x$的增大而增大;③若点$D$的横坐标最大值为5,则点$C的横坐标最小值为-5$;④当四边形$ACDB$为平行四边形时,$a= -\frac{4}{3}$.其中正确的是( )

A.②④
B.②③
C.①③④
D.①②④

答案： A

3. 已知:如图,在平面直角坐标系中,抛物线$y= ax^{2}+x的对称轴为直线x= 2$,顶点为$A$.点$P$为抛物线对称轴上一点,连结$OA$,$OP$.则当$OA\perp OP$时,点$P$的坐标为______.

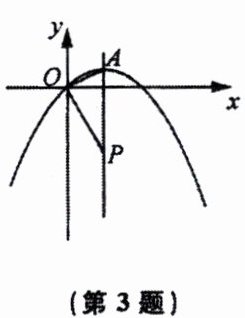
答案： (2,-4)

4. 如图,抛物线$y= -x^{2}+bx+c与x轴交于A(1,0)$,$B(-3,0)$两点,与$y轴相交于点C$,请完成下面的填空:
(1)该抛物线的解析式为______;
(2)在该抛物线的对称轴上存在一点$Q$,使得$\triangle QAC$的周长最小,则点$Q$的坐标为______;
(3)在抛物线上的第二象限上存在一点$P$,使$\triangle PBC$的面积最大,则点$P$的坐标为______,$\triangle PBC$的最大面积为______.

答案：
(1)y=-x²-2x+3；
(2)(-1,2)；
(3)(-3/2,15/4)，27/8

5. 如图,顶点坐标为$(1,9)的抛物线交x轴于点A(-2,0)$,点$B$两点,交$y轴于点C$,过$A,B,C三点的\odot O'交y轴于另一点D$,交抛物线于另一点$P$,过原点$O且垂直于AD的直线交AD于点H$,交$BC于点G$.
(1)求抛物线的解析式和点$G$的坐标;
(2)设直线$x= m交抛物线于点E$,交直线$OG于点F$,是否存在实数$m$,使$G,P,E,F$为一个平行四边形的四个顶点?如果存在,求出$m$的所有值;如果不存在,请说明理由.

答案：
(1)设抛物线解析式为y=a(x-1)²+9，把点A(-2,0)代入解析式，解得a=-1。因此函数解析式为y=-(x-1)²+9=-x²+2x+8。所以C(0,8)，B(4,0)。由相交弦定理，得|OA|·|OB|=|OC|·|OD|，即2×4=8×|OD|，|OD|=1。因为点D在y轴的负半轴上，所以点D的坐标为(0,-1)。在Rt△AOD中，OA=2，OD=1，OH⊥AD，所以由勾股定理得AD=√(2²+1²)=√5。又因为OA·OD=AD·OH，所以OH=2√5/5。因为OA²=AH·AD，即2²=AH·√5，所以AH=4√5/5。同理，由OD²=DH·AD，得DH=√5/5。设点H(x,y)，且x＜0，y＜0。在Rt△AOH中，AH·OH=|y|·OA，所以|y|=4/5，y=-4/5。在Rt△DOH中，DH·OH=|x|·OD，所以|x|=2/5，x=-2/5，所以点H的坐标是(-2/5,-4/5)。设直线OH的方程为y=kx(k≠0)，因为直线OH经过点H，所以解得k=2，所以直线OH的方程为y=2x。由对称得点P的坐标为(2,8)，设直线BC的方程为y=kx+b(k≠0)，则有{4k+b=0,b=8}，解得{k=-2,b=8}，所以直线BC的方程为y=-2x+8。联立方程组{y=-2x+8,y=2x}，解得{x=2,y=4}。所以点G的坐标为(2,4)。
(2)因为点P(2,8)，点G(2,4)，所以PG//EF。设点E的坐标为(m,-m²+2m+8)，点F的坐标为(m,2m)，要使四边形PGEF为平行四边形，已知PG//EF，尚需条件EF=PG，由|(-m²+2m+8)-2m|=|8-4|=4，得|-m²+8|=4，解得m=±2或m=±2√3，而m=2不合题意，舍去。所以存在实数m=-2或m=±2√3，使以P，G，E，F为顶点的四边形为平行四边形。