《2025年初中升高中衔接读本南京出版社数学》

15. 任何一个单位分数$\frac{1}{n}$都可以写成两个单位分数的和：$\frac{1}{n}= \frac{1}{p}+\frac{1}{q}$($n、p、q$都是正整数),显然,这里的$p、q都大于n$.如果设$p= n+a$,$q= n+b$,那么有$\frac{1}{n}= \frac{1}{n+a}+\frac{1}{n+b}$.
(1)探索上式中的正整数$a、b与正整数n$之间存在什么样的关系(写出推理过程)；
(2)写出$\frac{1}{6}$等于两个单位分数之和的所有可能情况.

答案： （1）因为$\frac{1}{n}=\frac{1}{n+a}+\frac{1}{n+b}$，所以$(n+a)(n+b)=n(n+a)+n(n+b)$，所以$n^{2}+nb+an+ab=n^{2}+na+n^{2}+nb$，所以$ab=n^{2}$.（2）由
(1)知$ab=n^{2},n=6$，所以$ab=36$，所以$a=1,2,3,4,6$，相对应的$b=36,18,12,9,6$，所以$\frac{1}{6}=\frac{1}{7}+\frac{1}{42}=\frac{1}{8}+\frac{1}{24}=\frac{1}{9}+\frac{1}{18}=\frac{1}{10}+\frac{15}{1}=\frac{1}{12}+\frac{1}{12}$.

16. 计算下列各题：
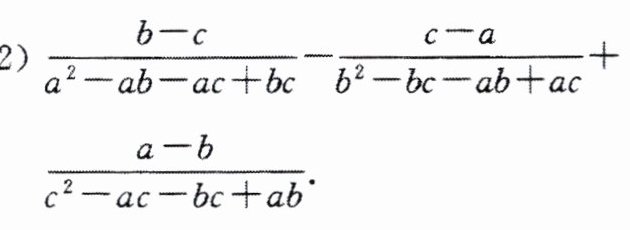
(1)$\frac{1}{x-1}-\frac{1}{1+x}-\frac{2}{x^2+1}-\frac{4}{x^4+1}-\frac{8}{x^8+1}$；
(2)$\frac{b-c}{a^2-ab-ac+bc}-\frac{c-a}{b^2-bc-ab+ac}+\frac{a-b}{c^2-ac-bc+ab}$.

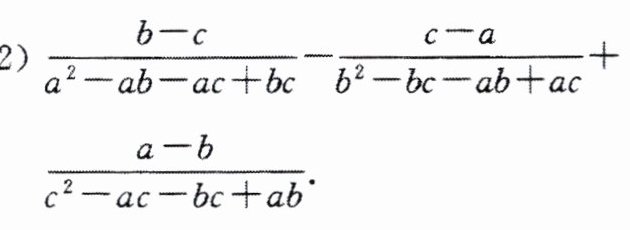
答案： （1）$\frac{16}{x^{16}-1}$（2）原式$=\frac{b-c}{(a-b)(a-c)}-\frac{c-a}{(b-c)(b-a)}+\frac{a-b}{(c-a)(c-b)}=\frac{1}{a-b}-\frac{1}{a-c}-\frac{1}{b-c}+\frac{1}{b-a}-\frac{1}{a-c}+\frac{1}{b-c}=-\frac{2}{a-c}$.

1. $\triangle ABC的三边长为a、b、c$,满足条件$\frac{2}{b}= \frac{1}{a}+\frac{1}{c}$,则边$b所对的角B$的大小是( )

A.锐角
B.直角
C.钝角
D.锐角、直角、钝角都有可能

答案： A

2. 已知$x-y+z= \frac{1}{x}-\frac{1}{y}+\frac{1}{z}= 1$,则( )

A.$x= 1,y= -1,z= 1$
B.$xyz= 1$
C.$x+y+z= 1$
D.$x= 1或y= -1或z= 1$

答案： D

3. 已知对于任意正整数$n$,都有$a_1+a_2+…+a_n= n^3$,则$\frac{1}{a_2-1}+\frac{1}{a_3-1}+…+\frac{1}{a_{100}-1}= $______.

答案： $\frac{33}{100}$

4. 不等于0的三个数$a、b、c满足\frac{1}{a}+\frac{1}{b}+\frac{1}{c}= \frac{1}{a+b+c}$,求证：$a、b、c$中至少有两个数互为相反数.

答案： 因为$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$，所以$\frac{bc+ac+ab}{abc}=\frac{1}{a+b+c}$，$bc(a+b+c)+ac(a+b+c)+ab(a+b+c)=abc$，所以$(b+c)a^{2}+(2bc+c^{2}+b^{2})a+bc^{2}+b^{2}c=0$，即$(a^{2}b+ab^{2})+(a^{2}c+ac^{2})+(abc+bc^{2})+(abc+b^{2}c)=0$，$ab(a+b)+ac(a+c)+bc(a+c)+bc(a+b)=0$，$(a+b)(ab+bc)+(a+c)(ac+bc)=0$，$b(a+b)(a+c)+c(a+c)(a+b)=0$，所以$(b+c)(a+b)(a+c)=0$，所以$b=-c$或$a=-b$或$a=-c$，即$a、b、c$中至少有两个数互为相反数.

5. 已知$\frac{(a-b)(b-c)(c-a)}{(a+b)(b+c)(c+a)}= \frac{5}{132}$,求$\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}$的值.

答案： 因为$\frac{a-b}{a+b}+\frac{b-c}{b+c}+\frac{c-a}{c+a}$$=\frac{(a-b)(b+c)(c+a)}{(a+b)(b+c)(c+a)}+\frac{(b-c)(a+b)(c+a)}{(a+b)(b+c)(c+a)}+\frac{(c-a)(a+b)(b+c)}{(a+b)(b+c)(c+a)}$$=\frac{(c+a)(2ab-2bc)+(c-a)(ab+b^{2}+ac+bc)}{(a+b)(b+c)(c+a)}$$=\frac{(a-c)(2bc+2ba-ab-b^{2}-ac-bc)}{(a+b)(b+c)(c+a)}$$=-\frac{(a-b)(b-c)(c-a)}{(a+b)(b+c)(c+a)}$$=-\frac{5}{132}$，所以$(\frac{a-b}{a+b}+1)+(\frac{b-c}{b+c}+1)+(\frac{c-a}{c+a}+1)=3-\frac{5}{132}=\frac{391}{132}$，即$\frac{2a}{a+b}+\frac{2b}{b+c}+\frac{2c}{c+a}=\frac{391}{132}$，所以$\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}=\frac{391}{264}$.