《2025年初中升高中衔接读本南京出版社数学》

1. 抛物线$y= (x-2)^2+3$的顶点坐标是( )

A.$(2,3)$
B.$(-2,3)$
C.$(2,-3)$
D.$(-2,-3)$

答案： A

2. 把抛物线$y= -x^2$向右平移1个单位长度,然后向下平移3个单位长度,则平移后抛物线的表达式为( )

A.$y= -(x-1)^2+3$
B.$y= -(x+1)^2+3$
C.$y= -(x-1)^2-3$
D.$y= -(x+1)^2-3$

答案： C

3. 对于二次函数$y= (x-1)^2+2$的图像,下列说法正确的是( )

A.开口向下
B.对称轴是$x= -1$
C.顶点坐标是$(1,2)$
D.与x轴有两个交点

答案： C

4. 已知反比例函数$y= \frac{a}{x}(a\neq0)$,当$x＞0$时,它的图像$y随x$的增大而减小,那么二次函数$y= ax^2-ax$的图像只可能是( )
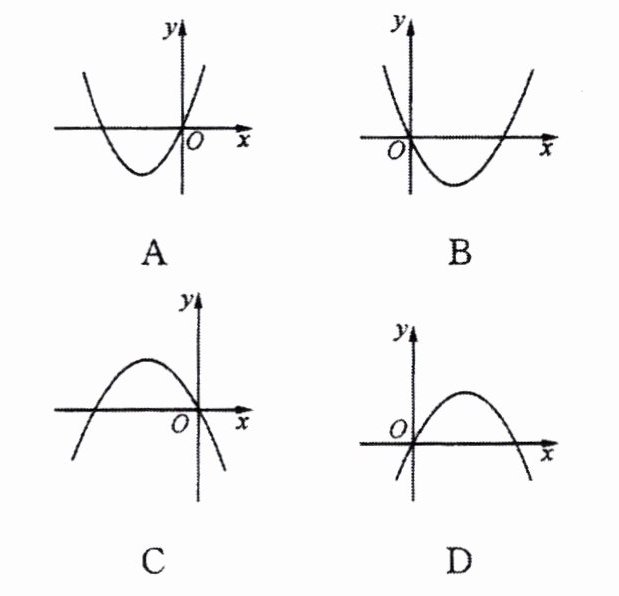
A
B
C
D

答案： B

5. 如图,平面直角坐标系中,点M是直线$y= 2$与x轴之间的一个动点,且点M是抛物线$y= \frac{1}{2}x^2+bx+c$的顶点,则方程$\frac{1}{2}x^2+bx+c= 1$的解的个数是( )


A.0或2
B.0或1
C.1或2
D.0,1或2

答案： D

6. 若抛物线$y= 2x^2-mx-m的对称轴是直线x= 2$,则$m= $______.

答案： 8

7. 已知抛物线$y= ax^2+bx+c$($a＞0$)的对称轴为直线$x= 1$,且经过点$(-1,y_1)$,$(2,y_2)$,试比较$y_1和y_2$的大小：$y_1$______$y_2$(填“＞”“＜”或“=”).

答案： ＞

8. 如图,抛物线与两坐标轴的交点坐标分别为$(-1,0)$,$(2,0)$,$(0,2)$,则抛物线的对称轴是______；若$y＞2$,则自变量$x$的取值范围是______.

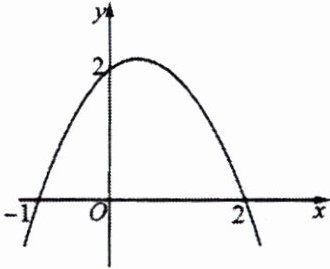
答案： $x=\frac{1}{2}$ $0＜x＜1$

9. 某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量$m$(件)与每件的销售价$x$(元)满足一次函数$m= 162-3x$,$30\leq x\leq54$.
(1)写出商场卖这种商品每天的销售利润$y与每件销售价x$之间的函数关系式；
(2)若商场要想每天获得最大销售利润,则每件商品的售价定为多少最合适？最大销售利润为多少？

答案： 【解析】（1）由已知得每件商品的销售利润为$(x - 30)$元，那么m件的销售利润为$y = m(x - 30)$，又$m = 162 - 3x$。$\therefore y=(x - 30)(162 - 3x)= - 3x^{2}+252x - 4860$，$30\leqslant x\leqslant 54$。（2）由（1）知对称轴为$x = 42$，位于x的范围内，另抛物线开口向下，$\therefore$当$x = 42$时，$y_{max} = - 3× 42^{2}+252× 42 - 4860 = 432$。$\therefore$当每件商品的售价定为42元时每天有最大销售利润，最大销售利润为432元。