《2025年暑假作业甘肃少年儿童出版社高一数学人教版》

1. 已知点 $ O, A, B, C $ 为空间不共面的四点, 且向量 $ \boldsymbol{a}= \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} $, 向量 $ \boldsymbol{b}= \overrightarrow{OA}+\overrightarrow{OB}-\overrightarrow{OC} $, 则与 $ \boldsymbol{a}, \boldsymbol{b} $ 不能构成空间基底的向量是 (C)
A.$ \overrightarrow{OA} $
B.$ \overrightarrow{OB} $
C.$ \overrightarrow{OC} $
D.$ \overrightarrow{OA} $ 或 $ \overrightarrow{OB} $

答案： 1. C

2. 若 $ \left\{\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \boldsymbol{e}_{3}\right\} $ 是空间向量的一个基底, 又 $ \boldsymbol{a}= \boldsymbol{e}_{1}+\boldsymbol{e}_{2}+\boldsymbol{e}_{3}, \boldsymbol{b}= \boldsymbol{e}_{1}+\boldsymbol{e}_{2}-\boldsymbol{e}_{3}, \boldsymbol{c}= \boldsymbol{e}_{1}-\boldsymbol{e}_{2}+\boldsymbol{e}_{3}, \boldsymbol{d}= \boldsymbol{e}_{1}+2 \boldsymbol{e}_{2}+3 \boldsymbol{e}_{3}, \boldsymbol{d}= x \boldsymbol{a}+y \boldsymbol{b}+z \boldsymbol{c} $, 则 $ x, y, z $ 的值分别为 ($\dfrac{5}{2}$，$-1$，$-\dfrac{1}{2}$)
A.$ \frac{5}{2},-1,-\frac{1}{2} $
B.$ -1, \frac{5}{2},-\frac{1}{2} $
C.$ \frac{5}{2}, 1, \frac{1}{2} $
D.$ -\frac{1}{2}, 1, \frac{5}{2} $

答案： 2. A 由题意得，$\boldsymbol {d}=x\boldsymbol {a}+y\boldsymbol {b}+z\boldsymbol {c}=x(\boldsymbol {e}_{1}+ \boldsymbol {e}_{2}+\boldsymbol {e}_{3})+y(\boldsymbol {e}_{1}+\boldsymbol {e}_{2}-\boldsymbol {e}_{3})+z(\boldsymbol {e}_{1}-\boldsymbol {e}_{2}+ \boldsymbol {e}_{3})=(x+y+z)\boldsymbol {e}_{1}+(x+y-z)\boldsymbol {e}_{2}+ (x-y+z)\boldsymbol {e}_{3}=\boldsymbol {e}_{1}+2\boldsymbol {e}_{2}+3\boldsymbol {e}_{3}$，由空间向量基本定理，得$\left\{\begin{array}{l} x+y+z=1\\ x+y-z=2\\ x-y+z=3\end{array}\right.$
解得$\left\{\begin{array}{l} x=\dfrac {5}{2}\\ y=-1\\ z=-\dfrac {1}{2}\end{array}\right.$

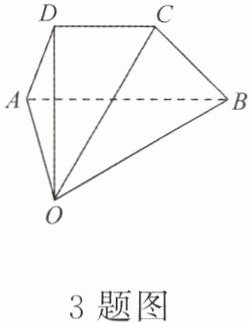
3. 如图, 梯形 $ ABCD $ 中, $ AB // CD, AB= 2 CD $, 点 $ O $ 为空间内任意一点, 设 $ \overrightarrow{OA}= \boldsymbol{a}, \overrightarrow{OB}= \boldsymbol{b}, \overrightarrow{OC}= \boldsymbol{c} $, 则向量 $ \overrightarrow{OD} $ 可用 $ \boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c} $ 表示为 (D)

A.$ \boldsymbol{a}-\boldsymbol{b}+2 \boldsymbol{c} $
B.$ \boldsymbol{a}-\boldsymbol{b}-2 \boldsymbol{c} $
C.$ -\frac{1}{2} \boldsymbol{a}+\frac{1}{2} \boldsymbol{b}+\boldsymbol{c} $
D.$ \frac{1}{2} \boldsymbol{a}-\frac{1}{2} \boldsymbol{b}+\boldsymbol{c} $ 

答案： 3. D

4. 如图是一个平行六面体 $ ABCD - A_{1} B_{1} C_{1} D_{1}, E $ 为 $ BC $ 延长线上一点, $ \overrightarrow{BC}= 2 \overrightarrow{CE} $, 则 $ \overrightarrow{D_{1} E}= $ (B)
A.$ \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_{1}} $
B.$ \overrightarrow{AB}+\frac{1}{2} \overrightarrow{AD}-\overrightarrow{AA_{1}} $
C.$ \overrightarrow{AB}+\overrightarrow{AD}-\overrightarrow{AA_{1}} $
D.$ \overrightarrow{AB}+\frac{1}{3} \overrightarrow{AD}-\overrightarrow{AA_{1}} $

答案： 4. B

5. 已知空间四边形 $ ABCD $ 中, $ \angle ACD= \angle BDC= 90^{\circ} $, 且 $ AB= 2, CD= 1 $, 则 $ AB $ 与 $ CD $ 所成的角是 (C)
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $

答案： 5. C

6. 点 $ P $ 是矩形 $ ABCD $ 所在平面外一点, 且 $ PA \perp $ 平面 $ ABCD, M, N $ 分别是 $ PC, PD $ 上的点, 且 $ \overrightarrow{PM}= \frac{2}{3} \overrightarrow{PC}, \overrightarrow{PN}= \overrightarrow{ND} $, 则满足 $ \overrightarrow{MN}= x \overrightarrow{AB}+y \overrightarrow{AD}+z \overrightarrow{AP} $ 的实数 $ x, y, z $ 的值分别为 ( )

A.$ -\frac{2}{3}, \frac{1}{6}, \frac{1}{6} $
B.$ \frac{2}{3},-\frac{1}{6}, \frac{1}{6} $
C.$ -\frac{2}{3}, \frac{1}{6},-\frac{1}{6} $
D.$ -\frac{2}{3},-\frac{1}{6}, \frac{1}{6} $

答案：
6. D 如图所示，取$PC$的中点$E$，连接$NE$，

则$\overrightarrow {MN}=\overrightarrow {EN}-\overrightarrow {EM}=\dfrac {1}{2}\overrightarrow {CD}-(\overrightarrow {PM}- \overrightarrow {PE})=\dfrac {1}{2}\overrightarrow {CD}-\left(\dfrac {2}{3}\overrightarrow {PC}-\dfrac {1}{2}\overrightarrow {PC}\right) $
$=\dfrac {1}{2}\overrightarrow {CD}-\dfrac {1}{6}\overrightarrow {PC} $
$=\dfrac {1}{2}\overrightarrow {AB}-\dfrac {1}{6}(-\overrightarrow {AP}+\overrightarrow {AB}+\overrightarrow {AD})=-\dfrac {2}{3}\overrightarrow {AB}-\dfrac {1}{6}\overrightarrow {AD}+\dfrac {1}{6}\overrightarrow {AP}$，又$\overrightarrow {MN}=x\overrightarrow {AB}+y\overrightarrow {AD}+z\overrightarrow {AP}$，
则$x=-\dfrac {2}{3}$，$y=-\dfrac {1}{6}$，$z=\dfrac {1}{6}$

7. (多选题) 设 $ x= \boldsymbol{a}+\boldsymbol{b}, y= \boldsymbol{b}+\boldsymbol{c}, z= \boldsymbol{c}+\boldsymbol{a} $, 且 $ \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\} $ 是空间的一个基底, 则下列向量组中, 可以作为空间一个基底的向量组有 (BCD)
A.$ \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{x}\} $
B.$ \{\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}\} $
C.$ \{\boldsymbol{b}, \boldsymbol{c}, \boldsymbol{z}\} $
D.$ \{\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}\} $

答案： 7. BCD

8. (多选题) 若 $ \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\} $ 构成空间的一个基底, 则下列向量共面的是 (ABD)
A.$ \boldsymbol{b}+\boldsymbol{c}, \boldsymbol{b}, \boldsymbol{b}-\boldsymbol{c} $
B.$ \boldsymbol{a}, \boldsymbol{a}+\boldsymbol{b}, \boldsymbol{a}-\boldsymbol{b} $
C.$ \boldsymbol{a}+\boldsymbol{b}, \boldsymbol{a}-\boldsymbol{b}, \boldsymbol{c} $
D.$ \boldsymbol{a}+\boldsymbol{b}, \boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}, \boldsymbol{c} $

答案： 8. ABD

9. 已知 $ a, b $ 是异面直线, $ A, B \in a, C, D \in b, A C \perp b, B D \perp b $, 且 $ A B= 2, C D= 1 $, 则 $ a, b $ 所成的角是 ______$60^{\circ }$.

答案： 9. 【解析】$\overrightarrow {AB}=\overrightarrow {AC}+\overrightarrow {CD}+\overrightarrow {DB}$，
所以$\overrightarrow {CD}\cdot \overrightarrow {AB}=\overrightarrow {CD}\cdot (\overrightarrow {AC}+\overrightarrow {CD}+ \overrightarrow {DB})=|\overrightarrow {CD}|^{2}=1$，
所以$\cos \langle \overrightarrow {CD},\overrightarrow {AB}\rangle =\dfrac {\overrightarrow {CD}\cdot \overrightarrow {AB}}{|\overrightarrow {CD}||\overrightarrow {AB}|}=\dfrac {1}{2}$，
所以异面直线$a$，$b$所成的角是$60^{\circ }$．
答案：$60^{\circ }$

10. 正方体 $ ABCD - A_{1} B_{1} C_{1} D_{1} $ 中, 点 $ E, F $ 分别是底面 $ A_{1} C_{1} $ 和侧面 $ C D_{1} $ 的中点, 若 $ \overrightarrow{EF}+\lambda \overrightarrow{A_{1} D}= \mathbf{0}(\lambda \in \mathbf{R}) $, 则 $ \lambda= $ ______$-\dfrac {1}{2}$.

答案： 10. $-\dfrac {1}{2}$

11. 在平行六面体 $ ABCD - A_{1} B_{1} C_{1} D_{1} $ 中, 若 $ \overrightarrow{A C_{1}}= x \overrightarrow{A B}+2 y \overrightarrow{B C}+3 z \overrightarrow{C_{1} C} $, 则 $ x + y + z= $ ______$\dfrac {11}{6}$.

答案： 11. $\dfrac {11}{6}$

12. 在正方体 $ ABCD - A_{1} B_{1} C_{1} D_{1} $ 中, 点 $ E, F $ 分别是底面 $ A_{1} B_{1} C_{1} D_{1} $ 和侧面 $ C_{1} D_{1} D C $ 的中心, 若 $ \overrightarrow{EF}+\lambda \overrightarrow{A_{1} D}= \mathbf{0}(\lambda \in \mathbf{R}) $, 则 $ \lambda= $ ______$-\dfrac {1}{2}$.

答案： 12. $-\dfrac {1}{2}$