《2025年暑假作业甘肃少年儿童出版社高一数学人教版》

18.(17分)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量(单位:辆)如下表: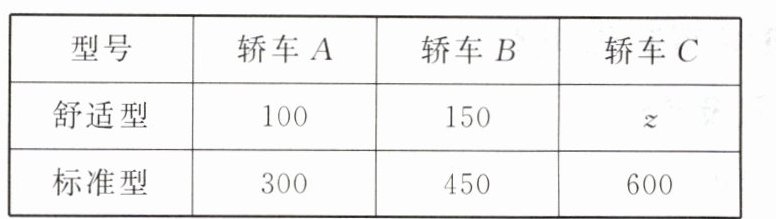
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值.
(2)用分层随机抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分为:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.

答案： 【解析】
(1)设该厂这个月共生产轿车n辆,由题意得$\frac {50}{n}=\frac {10}{100+300}$,所以$n=$$2000$.
则$z=2000-(100+300)-(150+450)$$-600=400.$
(2)设所抽样本中有a辆舒适型轿车,由题意得$\frac {400}{1000}=\frac {a}{5}$,即$a=2$.
因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车.
用$A_{1},A_{2}$表示2辆舒适型轿车,用$B_{1},B_{2},B_{3}$表示3辆标准型轿车,用E表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车",则试验的样本空间为$\Omega =\{ (A_{1},A_{2}),(A_{1},B_{1}),$$(A_{1},B_{2}),(A_{1},B_{3}),(A_{2},B_{1}),(A_{2},$$B_{2}),(A_{2},B_{3}),(B_{1},B_{2}),(B_{1},B_{3}),$$(B_{2},B_{3})\}$,共10个样本点.
事件E包含的样本点有:$(A_{1},A_{2})$,$(A_{1},B_{1}),(A_{1},B_{2}),(A_{1},B_{3}),(A_{2},$$B_{1}),(A_{2},B_{2}),(A_{2},B_{3})$,共7个.
故$P(E)=\frac {7}{10}$,即所求概率为$\frac {7}{10}$.
(3)样本平均数$\overline {x}=\frac {1}{8}×(9.4+8.6+$$9.2+9.6+8.7+9.3+9.0+8.2)$$=9$.
设D表示事件“从样本中任取一个数,该数与样本平均数之差的绝对值不超过0.5",则基本事件空间中有8个基本事件,事件D包含的基本事件为:9.4,8.6,9.2,8.7,9.3,9.0,共6个,所以$P(D)=\frac {6}{8}=\frac {3}{4}$,即所求概率为$\frac {3}{4}$.

19.(17分)某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组$[25,30)$,第2组$[30,35)$,第3组$[35,40)$,第4组$[40,45)$,第5组$[45,50]$,得到的频率分布直方图如图所示,如表是年龄的频数分布表.

(1)求正整数a,b,N的值.
a=25,b=100,N=250.
(2)现要从年龄较小的第1,2,3组中用分层随机抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是1,1,4.
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人年龄在第3组的概率.
恰有1人年龄在第3组的概率为$\frac{8}{15}$.

答案： 【解析】
(1)由频率分布直方图可知,$[25,30)$与$[30,35)$两组的人数相同，所以$a=25$,且$b=25×\frac {0.08}{0.02}=100$,总人数$N=\frac {25}{0.02×5}=250$.
(2)因为第1,2,3组共有$25+25+100$$=150$(人),
所以利用分层随机抽样的方法在150名员工中抽取6人,
第1组被抽取的人数为$6×\frac {25}{150}=1$,
第2组被抽取的人数为$6×\frac {25}{150}=1$,
第3组被抽取的人数为$6×\frac {100}{150}=4$,
所以年龄在第1,2,3组的人数分别是1,1,4.
(3)由
(2)可设第1组的1人为A,第2组的1人为B,第3组的4人分别为$C_{1},C_{2},C_{3},C_{4}$,
则从6人中随机抽取2人,样本空间$\Omega =\{ (A,B),(A,C_{1}),(A,C_{2}),(A,$$C_{3}),(A,C_{4}),(B,C_{1}),(B,C_{2}),(B,$$C_{3}),(B,C_{4}),(C_{1},C_{2}),(C_{1},C_{3}),(C_{1},$$C_{4}),(C_{2},C_{3}),(C_{2},C_{4}),(C_{3},C_{4})\}$,共有15个样本点.
其中恰有1人年龄在第3组的样本点为$(A,C_{1}),(A,C_{2}),(A,C_{3}),(A,C_{4})$,$(B,C_{1}),(B,C_{2}),(B,C_{3}),(B,C_{4})$,共有8个,
所以恰有1人年龄在第3组的概率为$\frac {8}{15}$.