《2025年暑假作业甘肃少年儿童出版社高一数学人教版》

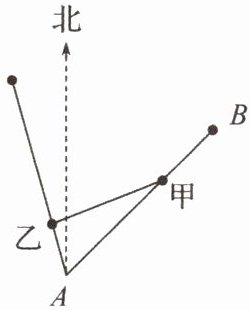
16. 已知海岛B在海岛A北偏东$45^{\circ }$,且与A相距20海里,船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时船乙从海岛A以4海里/小时的速度沿直线向北偏西$15^{\circ }$方向移动.
(1)求经过多长时间,船甲在船乙的正东方向.
(2)求甲从海岛B到达海岛A的过程中,甲乙两船的最短距离.

答案：
【解析】
(1)设经过$t(0＜t＜10)$小时，船甲移动到E的位置，船乙移动到F的位置，如图所示：

船甲与海岛A的距离为$AE=(20 - 2t)$海里，船乙与海岛A距离为$AF = 4t$海里.当甲在乙正东方时，$∠AFE = 75^{\circ}$，$∠AEF = 45^{\circ}$.在△AEF中，由正弦定理得：$\frac{AE}{\sin∠AFE}=\frac{AF}{\sin∠AEF}$，即$\frac{20 - 2t}{\sin75^{\circ}}=\frac{4t}{\sin45^{\circ}}$，则$t = 20 - 10\sqrt{3}$.答：经过$20 - 10\sqrt{3}$小时，船甲在船乙的正东方向.
(2)由
(1)得，$AE = 20 - 2t$，$AF = 4t$，由余弦定理得：$EF^{2}=AE^{2}+AF^{2}-2AE\cdot AF\cos∠EAF=(20 - 2t)^{2}+(4t)^{2}-2×(20 - 2t)×4t×\frac{1}{2}=28(t - \frac{20}{7})^{2}+\frac{1200}{7}$.由$0＜t＜10$，得当$t=\frac{20}{7}$时，$EF_{\min}=\frac{20\sqrt{21}}{7}$海里.答：甲、乙两船的最短距离为$\frac{20\sqrt{21}}{7}$海里.

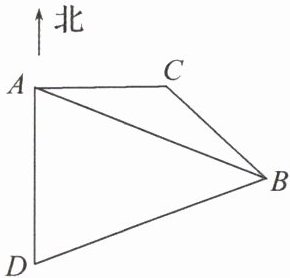
17. 某市发生水灾,国家应急管理部紧急从A处调飞机去某地运救灾物资到受灾的B处.现有以下两个方案供选择:
方案一:飞到位于A处正东方向上的C市调运救灾物资,再飞到B处;
方案二:飞到位于A处正南方向上的D市调运救灾物资,再飞到B处.
已知$AD= 500km,AB= 800km,∠ACB= 2∠DAB= 120^{\circ }$.
那么选择哪种方案,能使得飞行距离最短?
(参考数据:$\frac {\sqrt {3}}{3}\approx 0.577$)

答案： 【解析】方案一：在△ABC中，易知$∠CAB = 90^{\circ}-∠DAB = 30^{\circ}$，$∠ACB = 120^{\circ}$，$AB = 800km$，由$\frac{BC}{\sin∠CAB}=\frac{AB}{\sin∠ACB}$，得$BC=\frac{800\sqrt{3}}{3}km$.且△ABC为等腰三角形，所以$AC + BC = 2BC=\frac{1600\sqrt{3}}{3}(km)$.
方案二：在△ADB中，$∠DAB = 60^{\circ}$，$AD = 500km$，$AB = 800km$，所以$BD^{2}=AB^{2}+AD^{2}-2AB\cdot AD\cdot\cos∠DAB=800^{2}+500^{2}-2×800×500×\cos60^{\circ}=4.9×10^{5}$，所以$BD = 700km$，所以$BD + AD = 700 + 500 = 1200(km)$.因为$1200＞\frac{1600\sqrt{3}}{3}\approx923.2$，故选择方案一，能使飞行距离最短.