2025年暑假作业甘肃少年儿童出版社高一数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 在$\triangle ABC$中,$a= 7,b= 4\sqrt {3},c= \sqrt {13}$,则$\triangle ABC$的最小角为 (
A.$\frac {π}{3}$
B.$\frac {π}{6}$
C.$\frac {π}{4}$
D.$\frac {π}{12}$
B
)A.$\frac {π}{3}$
B.$\frac {π}{6}$
C.$\frac {π}{4}$
D.$\frac {π}{12}$
答案:
B 由三角形边角关系可知,角C为△ABC的最小角,则cosC=$\frac{a^{2}+b^{2}-c^{2}}{2ab}$=$\frac{7^{2}+(4\sqrt{3})^{2}-(\sqrt{13})^{2}}{2×7×4\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,所以C=$\frac{\pi}{6}$.
2. 在$\triangle ABC$中,$AB= 3$,AC边上的中线$BD= \sqrt {5},\overrightarrow {AC}\cdot \overrightarrow {AB}= 5$,则AC的长为 (
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:
B
3. 点P在平面上做匀速直线运动,速度$v= (4,-3)$,设开始时点P的坐标为$(-10,10)$,则5s后点P的坐标为(速度单位:m/s,长度单位:m) (
A.$(-2,4)$
B.$(-30,25)$
C.$(10,-5)$
D.$(5,-10)$
C
)A.$(-2,4)$
B.$(-30,25)$
C.$(10,-5)$
D.$(5,-10)$
答案:
C
4. 一物体在力F的作用下,由点$A(15,6)$移动到点$B(4,1)$,若$F= (1,-6)$,则F对物体所做的功为 (
A.-23
B.23
C.-19
D.19
19
)A.-23
B.23
C.-19
D.19
答案:
D因为$\overrightarrow{AB}=(-11,-5)$,$\overrightarrow{F}=(1,-6)$,所以$\overrightarrow{F}$对物体所做的功为$\overrightarrow{AB}\cdot\overrightarrow{F}=-11×1+(-5)×(-6)=19$.
5. $\triangle ABC的三边长分别为AB= 7,BC= 5,CA= 6$,则$\overrightarrow {AB}\cdot \overrightarrow {BC}$的值为 (
A.19
B.14
C.-18
D.-19
-19
)A.19
B.14
C.-18
D.-19
答案:
由余弦定理的推论知$\cos B=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB\cdot BC}=\frac{19}{35}$,所以$\overrightarrow{AB}\cdot\overrightarrow{BC}=|\overrightarrow{AB}||\overrightarrow{BC}|\cos(\pi - B)=7×5×(-\frac{19}{35})=-19$.
6. 东汉末年的数学家赵爽在《周髀算经》中利用一幅“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”.如图1,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.我们通过类比得到图2,它是由三个全等的钝角三角形与一个小等边三角形$A'B'C'$拼成的一个大等边三角形ABC,若$A'B'= 2,cos∠ABB'= \frac {11}{14}$,则$AB= $ (
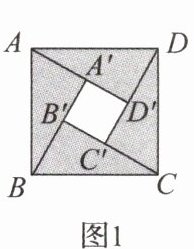
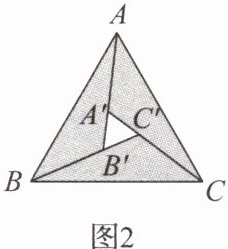
A.5
B.6
C.7
D.8
C
)

A.5
B.6
C.7
D.8
答案:
C
7. (多选题)小船被绳索拉向岸边,船在水中运动时,设水的阻力大小不变,那么小船匀速靠岸过程中,下列说法正确的是 (
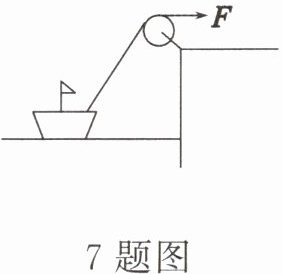
A.绳子的拉力不断增大
B.绳子的拉力不断变小
C.船所受浮力不断变小
D.船所受浮力保持不变
AC
)
A.绳子的拉力不断增大
B.绳子的拉力不断变小
C.船所受浮力不断变小
D.船所受浮力保持不变
答案:
AC设水的阻力为$f$,绳子的拉力为$F$,$F$与水平方向的夹角为$\theta$,$0<\theta<\frac{\pi}{2}$.则$|F|\cos\theta = |f|$,所以$|F|=\frac{|f|}{\cos\theta}$.因为$\theta$增大,$\cos\theta$减小,所以$|F|$增大.因为$|F|\sin\theta$增大,且船的重力为$|F|\sin\theta$与浮力之和,所以船所受浮力减小.
8. (多选题)在$\triangle ABC$中,角A,B,C所对的边分别为a,b,c,若$(a^{2}+c^{2}-b^{2})tanB= ac$,则角B的值为 (
A.$\frac {π}{6}$
B.$\frac {π}{3}$
C.$\frac {5π}{6}$
D.$\frac {2π}{3}$
AC
)A.$\frac {π}{6}$
B.$\frac {π}{3}$
C.$\frac {5π}{6}$
D.$\frac {2π}{3}$
答案:
1. 首先,根据余弦定理:
余弦定理公式为$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}$,则$a^{2}+c^{2}-b^{2}=2ac\cos B$。
2. 然后,将$a^{2}+c^{2}-b^{2}=2ac\cos B$代入已知条件$(a^{2}+c^{2}-b^{2})\tan B = ac$中:
得到$2ac\cos B\cdot\frac{\sin B}{\cos B}=ac$(因为$\tan B=\frac{\sin B}{\cos B}$)。
化简$2ac\cos B\cdot\frac{\sin B}{\cos B}=ac$,$ac\neq0$(三角形的边$a\gt0$,$c\gt0$),两边同时除以$ac$,可得$2\sin B = 1$。
所以$\sin B=\frac{1}{2}$。
3. 最后,根据角$B$的范围:
因为$B\in(0,\pi)$,且$\sin B=\frac{1}{2}$,所以$B = \frac{\pi}{6}$或$B=\frac{5\pi}{6}$。
综上,答案是AC。
余弦定理公式为$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}$,则$a^{2}+c^{2}-b^{2}=2ac\cos B$。
2. 然后,将$a^{2}+c^{2}-b^{2}=2ac\cos B$代入已知条件$(a^{2}+c^{2}-b^{2})\tan B = ac$中:
得到$2ac\cos B\cdot\frac{\sin B}{\cos B}=ac$(因为$\tan B=\frac{\sin B}{\cos B}$)。
化简$2ac\cos B\cdot\frac{\sin B}{\cos B}=ac$,$ac\neq0$(三角形的边$a\gt0$,$c\gt0$),两边同时除以$ac$,可得$2\sin B = 1$。
所以$\sin B=\frac{1}{2}$。
3. 最后,根据角$B$的范围:
因为$B\in(0,\pi)$,且$\sin B=\frac{1}{2}$,所以$B = \frac{\pi}{6}$或$B=\frac{5\pi}{6}$。
综上,答案是AC。
9. 在四边形ABCD中,已知$\overrightarrow {AB}= (4,-2),\overrightarrow {AC}= (7,4),\overrightarrow {AD}= (3,6)$,则四边形ABCD的面积是______
30
.
答案:
30
10. 在$\triangle ABC$中,角A,B,C的对边分别为a,b,c且$a= 3,b= 4,c= 6$,则$bccosA+accosB+abcosC$的值是______
$\frac{61}{2}$
.
答案:
【解析】$bc\cos A + ac\cos B + ab\cos C=\frac{b^{2}+c^{2}-a^{2}}{2}+\frac{a^{2}+c^{2}-b^{2}}{2}+\frac{a^{2}+b^{2}-c^{2}}{2}=\frac{a^{2}+b^{2}+c^{2}}{2}$.因为$a = 3$,$b = 4$,$c = 6$,所以$bc\cos A + ac\cos B + ab\cos C=\frac{1}{2}×(3^{2}+4^{2}+6^{2})=\frac{61}{2}$.答案:$\frac{61}{2}$
11. (2023·全国甲卷)在$\triangle ABC$中,$AB= 2,∠BAC= 60^{\circ },BC= \sqrt {6}$,D为BC上一点,AD为$∠BAC$的平分线,则$AD= $______.
答案:
【解析】如图所示,记$AB = c$,$AC = b$,$BC = a$.

方法一:由余弦定理可得,$2^{2}+b^{2}-2×2×b×\cos60^{\circ}=6$,因为$b>0$,所以$b = 1 + \sqrt{3}$.由$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$可得,$\frac{1}{2}×2×b×\sin60^{\circ}=\frac{1}{2}×2×AD×\sin30^{\circ}+\frac{1}{2}×AD×b×\sin30^{\circ}$,解得$AD=\frac{\sqrt{3}b}{1+\frac{b}{2}}=\frac{2\sqrt{3}(1+\sqrt{3})}{3+\sqrt{3}}=2$.
方法二:由余弦定理可得,$2^{2}+b^{2}-2×2×b×\cos60^{\circ}=6$,因为$b>0$,所以$b = 1 + \sqrt{3}$.由正弦定理可得,$\frac{\sqrt{6}}{\sin60^{\circ}}=\frac{b}{\sin B}=\frac{2}{\sin C}$,解得$\sin B=\frac{\sqrt{6}+\sqrt{2}}{4}$,$\sin C=\frac{\sqrt{2}}{2}$.因为$1 + \sqrt{3}>\sqrt{6}>2$,所以$C = 45^{\circ}$,$B = 180^{\circ}-60^{\circ}-45^{\circ}=75^{\circ}$.又$∠BAD = 30^{\circ}$,所以$∠ADB = 75^{\circ}$,即$AD = AB = 2$.答案:2
【解析】如图所示,记$AB = c$,$AC = b$,$BC = a$.

方法一:由余弦定理可得,$2^{2}+b^{2}-2×2×b×\cos60^{\circ}=6$,因为$b>0$,所以$b = 1 + \sqrt{3}$.由$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$可得,$\frac{1}{2}×2×b×\sin60^{\circ}=\frac{1}{2}×2×AD×\sin30^{\circ}+\frac{1}{2}×AD×b×\sin30^{\circ}$,解得$AD=\frac{\sqrt{3}b}{1+\frac{b}{2}}=\frac{2\sqrt{3}(1+\sqrt{3})}{3+\sqrt{3}}=2$.
方法二:由余弦定理可得,$2^{2}+b^{2}-2×2×b×\cos60^{\circ}=6$,因为$b>0$,所以$b = 1 + \sqrt{3}$.由正弦定理可得,$\frac{\sqrt{6}}{\sin60^{\circ}}=\frac{b}{\sin B}=\frac{2}{\sin C}$,解得$\sin B=\frac{\sqrt{6}+\sqrt{2}}{4}$,$\sin C=\frac{\sqrt{2}}{2}$.因为$1 + \sqrt{3}>\sqrt{6}>2$,所以$C = 45^{\circ}$,$B = 180^{\circ}-60^{\circ}-45^{\circ}=75^{\circ}$.又$∠BAD = 30^{\circ}$,所以$∠ADB = 75^{\circ}$,即$AD = AB = 2$.答案:2
12. 如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角$∠ABC= 120^{\circ }$;从B处攀登4千米到达D处,回头看索道AC,发现张角$∠ADC= 150^{\circ }$;从D处再攀登8千米方到达C处,则索道AC的长为
$4\sqrt{13}$
千米.
答案:
$4\sqrt{13}$
查看更多完整答案,请扫码查看


