2025年暑假作业甘肃少年儿童出版社高一数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
9.把一个棱长为a的正方体,切成27个全等的小正方体后,表面积增加了
12a²
.
答案:
【解析】原正方体的棱长为 $ a $,表面积为 $ S = 6 a ^ { 2 } $,切成的 $ 27 $ 个小正方体的棱长为 $ \frac { 1 } { 3 } a $,每个小正方体的表面积 $ S _ { 1 } = \frac { 1 } { 9 } a ^ { 2 } × 6 = \frac { 2 } { 3 } a ^ { 2 } $,所以 $ 27 $ 个小正方体的表面积是 $ \frac { 2 } { 3 } a ^ { 2 } × 27 = 18 a ^ { 2 } $,表面积增加了 $ 12 a ^ { 2 } $。答案:$ 12 a ^ { 2 } $
10.长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为______
14π
.
答案:
$ 14 \pi $
11.如图所示,正方体ABCD-$A_{1}B_{1}C_{1}D_{1}$的棱长为1,E为线段$B_{1}C$上的一点,则三棱锥A-$DED_{1}$的体积为______
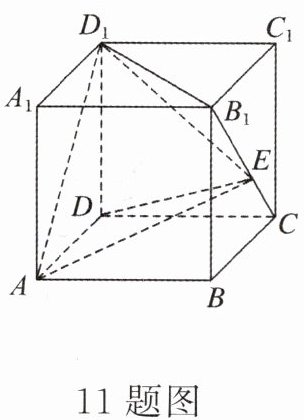
$\frac{1}{6}$
.
答案:
$ \frac { 1 } { 6 } $
12.如图,已知圆锥PO的底面半径OA的长度为1,母线PA的长度为2,半径为$R_{1}的球O_{1}$与圆锥的侧面相切,并与底面相切于点O,则$R_{1}$= ______;若球$O_{2}与球O_{1}$、圆锥的底面和侧面均相切,则球$O_{2}$的表面积为______.

答案:
【解析】该几何体的轴截面如图所示,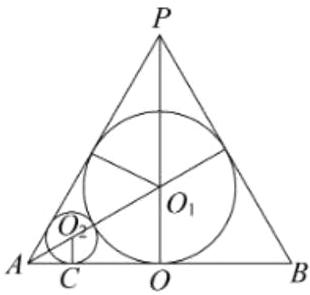
由题意可知 $ \triangle P A B $ 为等边三角形,且边长为 $ 2 $,圆 $ O _ { 1 } $ 与三角形的三边都相切,圆 $ O _ { 1 } $ 的半径等于球 $ O _ { 1 } $ 的半径为 $ R _ { 1 } $,则 $ \frac { 1 } { 2 } ( 2 + 2 + 2 ) R _ { 1 } = \frac { 1 } { 2 } × 2 × 2 \sin 60 ^ { \circ } $,解得 $ R _ { 1 } = \frac { \sqrt { 3 } } { 3 } $,因为 $ \angle O _ { 1 } A O = 30 ^ { \circ } $,所以 $ A O _ { 2 } = 2 O _ { 2 } C = 2 R _ { 2 } $,$ A O _ { 1 } = 2 O O _ { 1 } = 2 R _ { 1 } $,因为 $ A O _ { 1 } = A O _ { 2 } + O _ { 2 } O _ { 1 } $,所以 $ 2 R _ { 1 } = 2 R _ { 2 } + R _ { 2 } + R _ { 1 } $,所以 $ R _ { 2 } = \frac { 1 } { 3 } R _ { 1 } = \frac { \sqrt { 3 } } { 9 } $,所以球 $ O _ { 2 } $ 的表面积为 $ 4 \pi R _ { 2 } ^ { 2 } = 4 \pi \left( \frac { \sqrt { 3 } } { 9 } \right) ^ { 2 } = \frac { 4 } { 27 } \pi $。答案:$ \frac { \sqrt { 3 } } { 3 } $ $ \frac { 4 } { 27 } \pi $
【解析】该几何体的轴截面如图所示,

由题意可知 $ \triangle P A B $ 为等边三角形,且边长为 $ 2 $,圆 $ O _ { 1 } $ 与三角形的三边都相切,圆 $ O _ { 1 } $ 的半径等于球 $ O _ { 1 } $ 的半径为 $ R _ { 1 } $,则 $ \frac { 1 } { 2 } ( 2 + 2 + 2 ) R _ { 1 } = \frac { 1 } { 2 } × 2 × 2 \sin 60 ^ { \circ } $,解得 $ R _ { 1 } = \frac { \sqrt { 3 } } { 3 } $,因为 $ \angle O _ { 1 } A O = 30 ^ { \circ } $,所以 $ A O _ { 2 } = 2 O _ { 2 } C = 2 R _ { 2 } $,$ A O _ { 1 } = 2 O O _ { 1 } = 2 R _ { 1 } $,因为 $ A O _ { 1 } = A O _ { 2 } + O _ { 2 } O _ { 1 } $,所以 $ 2 R _ { 1 } = 2 R _ { 2 } + R _ { 2 } + R _ { 1 } $,所以 $ R _ { 2 } = \frac { 1 } { 3 } R _ { 1 } = \frac { \sqrt { 3 } } { 9 } $,所以球 $ O _ { 2 } $ 的表面积为 $ 4 \pi R _ { 2 } ^ { 2 } = 4 \pi \left( \frac { \sqrt { 3 } } { 9 } \right) ^ { 2 } = \frac { 4 } { 27 } \pi $。答案:$ \frac { \sqrt { 3 } } { 3 } $ $ \frac { 4 } { 27 } \pi $
13.某个实心零部件的形状是如图所示的几何体,其下部是底面均为正方形,侧面为全等的等腰梯形的四棱台$A_{1}B_{1}C_{1}D_{1}$-ABCD,其上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-$A_{2}B_{2}C_{2}D_{2}$.现需对该零部件表面进行防腐处理,已知AB= 10,$A_{1}B_{1}$= 20,$AA_{2}$= 30,$AA_{1}$= 13(单位:cm),若加工处理费为0.2元/$cm^{2}$,则需支付加工处理费多少元?


答案:
解:
上部四棱柱表面积 $ S_1 $
四棱柱 $ ABCD-A_2B_2C_2D_2 $ 上底面为正方形,侧面为矩形。
- 上底面面积:$ A_2B_2^2 = AB^2 = 10^2 = 100 \, \text{cm}^2 $
- 侧面面积:$ 4 × AB × AA_2 = 4 × 10 × 30 = 1200 \, \text{cm}^2 $
- $ S_1 = 100 + 1200 = 1300 \, \text{cm}^2 $
下部四棱台表面积 $ S_2 $
四棱台 $ A_1B_1C_1D_1-ABCD $ 下底面为正方形,侧面为等腰梯形。
- 下底面面积:$ A_1B_1^2 = 20^2 = 400 \, \text{cm}^2 $
- 侧面等腰梯形高:$ h = \sqrt{AA_1^2 - \left( \frac{A_1B_1 - AB}{2} \right)^2} = \sqrt{13^2 - \left( \frac{20 - 10}{2} \right)^2} = \sqrt{169 - 25} = 12 \, \text{cm} $
- 侧面面积:$ 4 × \frac{1}{2} × (AB + A_1B_1) × h = 4 × \frac{1}{2} × (10 + 20) × 12 = 720 \, \text{cm}^2 $
- $ S_2 = 400 + 720 = 1120 \, \text{cm}^2 $
零部件总表面积 $ S $
$ S = S_1 + S_2 = 1300 + 1120 = 2420 \, \text{cm}^2 $
加工处理费
$ 0.2 × 2420 = 484 \, \text{元} $
答:需支付加工处理费 484 元。
上部四棱柱表面积 $ S_1 $
四棱柱 $ ABCD-A_2B_2C_2D_2 $ 上底面为正方形,侧面为矩形。
- 上底面面积:$ A_2B_2^2 = AB^2 = 10^2 = 100 \, \text{cm}^2 $
- 侧面面积:$ 4 × AB × AA_2 = 4 × 10 × 30 = 1200 \, \text{cm}^2 $
- $ S_1 = 100 + 1200 = 1300 \, \text{cm}^2 $
下部四棱台表面积 $ S_2 $
四棱台 $ A_1B_1C_1D_1-ABCD $ 下底面为正方形,侧面为等腰梯形。
- 下底面面积:$ A_1B_1^2 = 20^2 = 400 \, \text{cm}^2 $
- 侧面等腰梯形高:$ h = \sqrt{AA_1^2 - \left( \frac{A_1B_1 - AB}{2} \right)^2} = \sqrt{13^2 - \left( \frac{20 - 10}{2} \right)^2} = \sqrt{169 - 25} = 12 \, \text{cm} $
- 侧面面积:$ 4 × \frac{1}{2} × (AB + A_1B_1) × h = 4 × \frac{1}{2} × (10 + 20) × 12 = 720 \, \text{cm}^2 $
- $ S_2 = 400 + 720 = 1120 \, \text{cm}^2 $
零部件总表面积 $ S $
$ S = S_1 + S_2 = 1300 + 1120 = 2420 \, \text{cm}^2 $
加工处理费
$ 0.2 × 2420 = 484 \, \text{元} $
答:需支付加工处理费 484 元。
14.如图,已知直角梯形ABCD,BC//AD,∠ABC= 90°,AB= 5,BC= 16,AD= 4.求:
(1)以AB所在直线为轴旋转一周所得几何体的表面积.
(2)以BC所在直线为轴旋转一周所得几何体的表面积.

(1)以AB所在直线为轴旋转一周所得几何体的表面积.
(2)以BC所在直线为轴旋转一周所得几何体的表面积.

答案:
【解析】
(1) 以 $ A B $ 所在直线为轴旋转一周所得的几何体是圆台,其上底面半径是 $ 4 $,下底面半径是 $ 16 $,母线 $ D C = \sqrt { 5 ^ { 2 } + ( 16 - 4 ) ^ { 2 } } = 13 $。故该几何体的表面积为 $ \pi ( 4 + 16 ) × 13 + \pi × 4 ^ { 2 } + \pi × 16 ^ { 2 } = 532 \pi $。
(2) 以 $ B C $ 所在直线为轴旋转一周所得的几何体是圆柱和圆锥的组合体,如图.
其中圆锥的高为 $ 16 - 4 = 12 $,圆柱的母线长为 $ A D = 4 $,故该几何体的表面积为 $ 2 \pi × 5 × 4 + \pi × 5 ^ { 2 } + \pi × 5 × 13 = 130 \pi $。
【解析】
(1) 以 $ A B $ 所在直线为轴旋转一周所得的几何体是圆台,其上底面半径是 $ 4 $,下底面半径是 $ 16 $,母线 $ D C = \sqrt { 5 ^ { 2 } + ( 16 - 4 ) ^ { 2 } } = 13 $。故该几何体的表面积为 $ \pi ( 4 + 16 ) × 13 + \pi × 4 ^ { 2 } + \pi × 16 ^ { 2 } = 532 \pi $。
(2) 以 $ B C $ 所在直线为轴旋转一周所得的几何体是圆柱和圆锥的组合体,如图.

其中圆锥的高为 $ 16 - 4 = 12 $,圆柱的母线长为 $ A D = 4 $,故该几何体的表面积为 $ 2 \pi × 5 × 4 + \pi × 5 ^ { 2 } + \pi × 5 × 13 = 130 \pi $。
15.如图,三棱锥A-BCD中,AD,BD,CD两两垂直,AD= 1,BD= CD= 2.
(1)求该几何体外接球的体积;
(2)求该几何体内切球的半径.
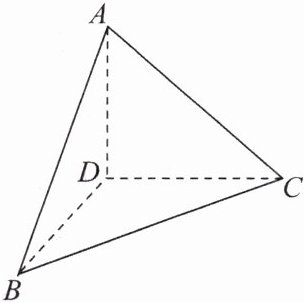
(1)求该几何体外接球的体积;
(2)求该几何体内切球的半径.

答案:
【解析】
(1) 以 $ D C $,$ D B $,$ D A $ 为长、宽、高构造一个长方体,则该长方体的外接球就是该三棱锥的外接球,即外接球的半径 $ R = \frac { 1 } { 2 } \sqrt { 2 ^ { 2 } + 2 ^ { 2 } + 1 ^ { 2 } } = \frac { 3 } { 2 } $,所以该几何体外接球的体积 $ V = \frac { 4 } { 3 } \pi R ^ { 3 } = \frac { 9 } { 2 } \pi $。
(2) 设内切球的球心为 $ O $,半径为 $ r $,则 $ V _ { A - B C D } = V _ { O - A D B } + V _ { O - A D C } + V _ { O - D C B } + V _ { O - A B C } $。即 $ \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × 2 × 1 = \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × 2 r + \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × r + \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × r + \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 \sqrt { 2 } × \sqrt { 3 } r $,得 $ r = \frac { 2 } { 4 + \sqrt { 6 } } = \frac { 4 - \sqrt { 6 } } { 5 } $。所以该几何体内切球的半径为 $ \frac { 4 - \sqrt { 6 } } { 5 } $。
(1) 以 $ D C $,$ D B $,$ D A $ 为长、宽、高构造一个长方体,则该长方体的外接球就是该三棱锥的外接球,即外接球的半径 $ R = \frac { 1 } { 2 } \sqrt { 2 ^ { 2 } + 2 ^ { 2 } + 1 ^ { 2 } } = \frac { 3 } { 2 } $,所以该几何体外接球的体积 $ V = \frac { 4 } { 3 } \pi R ^ { 3 } = \frac { 9 } { 2 } \pi $。
(2) 设内切球的球心为 $ O $,半径为 $ r $,则 $ V _ { A - B C D } = V _ { O - A D B } + V _ { O - A D C } + V _ { O - D C B } + V _ { O - A B C } $。即 $ \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × 2 × 1 = \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × 2 r + \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × r + \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 × r + \frac { 1 } { 3 } × \frac { 1 } { 2 } × 2 \sqrt { 2 } × \sqrt { 3 } r $,得 $ r = \frac { 2 } { 4 + \sqrt { 6 } } = \frac { 4 - \sqrt { 6 } } { 5 } $。所以该几何体内切球的半径为 $ \frac { 4 - \sqrt { 6 } } { 5 } $。
查看更多完整答案,请扫码查看


