2025年暑假作业甘肃少年儿童出版社高一数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
14.从某珍珠公司生产的产品中,任意抽取12颗珍珠,得到它们的质量(单位:g)如下:
7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
(1)分别求出这组数据的第25,50,75,95百分位数.
(2)请你找出珍珠质量较小的前15%的珍珠质量.
(3)若用第25,50,95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.
7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
(1)分别求出这组数据的第25,50,75,95百分位数.
(2)请你找出珍珠质量较小的前15%的珍珠质量.
(3)若用第25,50,95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.
答案:
【解析】
(1)将所有数据从小到大排列,得7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9。因为共有12个数据,所以12×25% = 3,12×50% = 6,12×75% = 9,12×95% = 11.4。则第25百分位数是$\frac{8.0+8.3}{2}$=8.15,第50百分位数是$\frac{8.5+8.5}{2}$ = 8.5,第75百分位数是$\frac{8.6+8.9}{2}$=8.75,第95百分位数是第12个数据9.9。
(2)因为共有12个数据,所以12×15% = 1.8,则第15百分位数是第2个数据7.9。即产品质量较小的前15%的产品有2个,它们的质量分别为7.8,7.9。
(3)由
(1)可知样本数据的第25百分位数是8.15g,第50百分位数为8.5g,第95百分位数是9.9g,所以质量小于或等于8.15g的珍珠为次品,质量大于8.15g且小于或等于8.5g的珍珠为合格品,质量大于8.5g 且小于或等于9.9g的珍珠为优等品,质量大于9.9g的珍珠为特优品。
(1)将所有数据从小到大排列,得7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9。因为共有12个数据,所以12×25% = 3,12×50% = 6,12×75% = 9,12×95% = 11.4。则第25百分位数是$\frac{8.0+8.3}{2}$=8.15,第50百分位数是$\frac{8.5+8.5}{2}$ = 8.5,第75百分位数是$\frac{8.6+8.9}{2}$=8.75,第95百分位数是第12个数据9.9。
(2)因为共有12个数据,所以12×15% = 1.8,则第15百分位数是第2个数据7.9。即产品质量较小的前15%的产品有2个,它们的质量分别为7.8,7.9。
(3)由
(1)可知样本数据的第25百分位数是8.15g,第50百分位数为8.5g,第95百分位数是9.9g,所以质量小于或等于8.15g的珍珠为次品,质量大于8.15g且小于或等于8.5g的珍珠为合格品,质量大于8.5g 且小于或等于9.9g的珍珠为优等品,质量大于9.9g的珍珠为特优品。
15.为满足广大市民的日常生活所需,某快递公司以优厚的条件招聘派送员,现给出了两种日薪方案.
甲方案:底薪100元,每派送一单奖励1元.
乙方案:底薪150元,每日前55单没有奖励,超过55单的部分每单奖励10元.
(1)请分别求出这两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员10天的派送记录,得到派送员的日均派送单数与天数如表.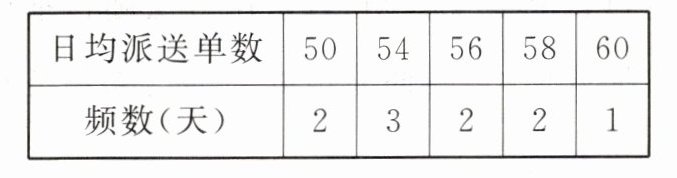
回答下列问题:
①根据以上数据,设每名派送员的日薪为x(单位:元),试分别求出这10天中甲、乙两种方案的日薪x的平均数及方差;
②结合①中的数据,根据统计学的思想,若你去应聘派送员,选择哪种薪酬方案比较合适?并说明你的理由.
甲方案:底薪100元,每派送一单奖励1元.
乙方案:底薪150元,每日前55单没有奖励,超过55单的部分每单奖励10元.
(1)请分别求出这两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员10天的派送记录,得到派送员的日均派送单数与天数如表.

回答下列问题:
①根据以上数据,设每名派送员的日薪为x(单位:元),试分别求出这10天中甲、乙两种方案的日薪x的平均数及方差;
②结合①中的数据,根据统计学的思想,若你去应聘派送员,选择哪种薪酬方案比较合适?并说明你的理由.
答案:
【解析】
(1)由题意可知,甲方案日薪y与送货单数n的函数关系式为y = n×1+100=n+100,n∈N。对于乙方案,当n≤55,n∈N时,y =150;当n>55,n∈N时,y=150+(n−55)×10=10n−400。故乙方案日薪y与送货单数n的函数关系式为$y = \begin{cases} 150, n \leq 55, n \in N, \\ 10n - 400, n > 55, n \in N. \end{cases}$
(2)①甲方案日薪x的平均数$\overline{x}_{甲} = \frac{150 × 2 + 154 × 3 + 156 × 2 + 158 × 2 + 160 × 1}{10} = 155$(元),方差$s_{甲}^2 = \frac{1}{10} × [2 × (150 - 155)^2 + 3 × (154 - 155)^2 + 2 × (156 - 155)^2 + 2 × (158 - 155)^2 + (160 - 155)^2] = \frac{1}{10} × (50 + 3 + 2 + 18 + 25) = 9.8$。乙方案日薪x的平均数$\overline{x}_{乙} = \frac{150 × 2 + 150 × 3 + 160 × 2 + 180 × 2 + 200}{10} = 163$(元),方差$s_{乙}^2 = \frac{1}{10} × [2 × (150 - 163)^2 + 3 × (150 - 163)^2 + 2 × (160 - 163)^2 + 2 × (180 - 163)^2 + (200 - 163)^2] = \frac{1}{10} × (338 + 507 + 18 + 578 + 1369) = 281$。
②由①可知,$\overline{x}_{甲} < \overline{x}_{乙}$,则选择乙方案比较合适。(或由①可知,$\overline{x}_{甲} < \overline{x}_{乙}$,但二者相差不大,且$s_{乙}^2 > s_{甲}^2$,二者相差较大,即甲方案日薪波动情况比乙小得多,则选择甲方案比较合适。)
(1)由题意可知,甲方案日薪y与送货单数n的函数关系式为y = n×1+100=n+100,n∈N。对于乙方案,当n≤55,n∈N时,y =150;当n>55,n∈N时,y=150+(n−55)×10=10n−400。故乙方案日薪y与送货单数n的函数关系式为$y = \begin{cases} 150, n \leq 55, n \in N, \\ 10n - 400, n > 55, n \in N. \end{cases}$
(2)①甲方案日薪x的平均数$\overline{x}_{甲} = \frac{150 × 2 + 154 × 3 + 156 × 2 + 158 × 2 + 160 × 1}{10} = 155$(元),方差$s_{甲}^2 = \frac{1}{10} × [2 × (150 - 155)^2 + 3 × (154 - 155)^2 + 2 × (156 - 155)^2 + 2 × (158 - 155)^2 + (160 - 155)^2] = \frac{1}{10} × (50 + 3 + 2 + 18 + 25) = 9.8$。乙方案日薪x的平均数$\overline{x}_{乙} = \frac{150 × 2 + 150 × 3 + 160 × 2 + 180 × 2 + 200}{10} = 163$(元),方差$s_{乙}^2 = \frac{1}{10} × [2 × (150 - 163)^2 + 3 × (150 - 163)^2 + 2 × (160 - 163)^2 + 2 × (180 - 163)^2 + (200 - 163)^2] = \frac{1}{10} × (338 + 507 + 18 + 578 + 1369) = 281$。
②由①可知,$\overline{x}_{甲} < \overline{x}_{乙}$,则选择乙方案比较合适。(或由①可知,$\overline{x}_{甲} < \overline{x}_{乙}$,但二者相差不大,且$s_{乙}^2 > s_{甲}^2$,二者相差较大,即甲方案日薪波动情况比乙小得多,则选择甲方案比较合适。)
查看更多完整答案,请扫码查看


