2025年暑假作业甘肃少年儿童出版社高一数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 袋内有3个白球和2个黑球,从中有放回地摸球,用A表示“第一次摸到白球”,如果“第二次摸到白球”记为B,否则记为C,那么事件A与B,A与C的关系是 (
A.A与B,A与C均相互独立
B.A与B相互独立,A与C互斥
C.A与B,A与C均互斥
D.A与B互斥,A与C相互独立
A
)A.A与B,A与C均相互独立
B.A与B相互独立,A与C互斥
C.A与B,A与C均互斥
D.A与B互斥,A与C相互独立
答案:
A 由于摸球过程是有放回的,所以第一次摸球的结果对第二次摸球的结果没有影响,故事件 $ A $ 与 $ B $,$ A $ 与 $ C $ 均相互独立,且 $ A $ 与 $ B $,$ A $ 与 $ C $ 均有可能同时发生,说明 $ A $ 与 $ B $,$ A $ 与 $ C $ 均不互斥。
2. 如图所示,A,B,C表示3个开关,若在某段时间内,它们正常工作的概率分别为0.9,0.8,0.7,则该系统的可靠性(3个开关只要一个开关正常工作即可靠)为 (
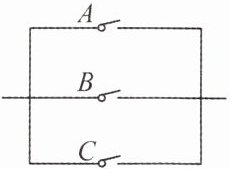
A.0.504
B.0.994
C.0.496
D.0.064
B
)
A.0.504
B.0.994
C.0.496
D.0.064
答案:
B
3. 已知A,B是相互独立事件,若$P(A)= 0.2$,$P(AB+\overline {A}B+A\overline {B})= 0.44$,则$P(B)$等于 (
A.0.3
B.0.4
C.0.5
D.0.6
0.3
)A.0.3
B.0.4
C.0.5
D.0.6
答案:
A 因为 $ A $,$ B $ 是相互独立事件,所以 $ \overline{A} $,$ B $ 和 $ A $,$ \overline{B} $ 均相互独立。因为 $ P(A)=0.2 $,$ P(AB+\overline{A}B+A\overline{B}) = 0.44 $,所以 $ P(A)P(B)+P(\overline{A})P(B)+P(A)P(\overline{B}) = 0.44 $,所以 $ 0.2P(B)+0.8P(B)+0.2[1 - P(B)] = 0.44 $,解得 $ P(B)=0.3 $。
4. 打靶时,甲每打10次可中靶8次,乙每打10次可中靶7次,两人互不干扰,若两人同时射击一次,则他们都中靶的概率是 (
A.$\frac {14}{25}$
B.$\frac {12}{25}$
C.$\frac {3}{4}$
D.$\frac {3}{5}$
A
)A.$\frac {14}{25}$
B.$\frac {12}{25}$
C.$\frac {3}{4}$
D.$\frac {3}{5}$
答案:
A
5. 社区开展“军事知识竞赛”,甲、乙两人能获得一等奖的概率分别为$\frac {3}{5}和\frac {2}{3}$,两人是否获得一等奖相互独立,则这两人中至少有一人获得一等奖的概率为 (
A.$\frac {3}{5}$
B.$\frac {2}{15}$
C.$\frac {13}{15}$
D.$\frac {8}{15}$
$\frac{13}{15}$
)A.$\frac {3}{5}$
B.$\frac {2}{15}$
C.$\frac {13}{15}$
D.$\frac {8}{15}$
答案:
C 由题意可知,甲、乙两人都不能获得一等奖的概率为 $ (1 - \frac{3}{5})×(1 - \frac{2}{3}) = \frac{2}{15} $,故这两人中至少有一人获得一等奖的概率为 $ 1 - \frac{2}{15} = \frac{13}{15} $。
6. 先后抛掷硬币三次,则至少一次正面朝上的概率是 (
A.$\frac {1}{8}$
B.$\frac {3}{8}$
C.$\frac {5}{8}$
D.$\frac {7}{8}$
D
)A.$\frac {1}{8}$
B.$\frac {3}{8}$
C.$\frac {5}{8}$
D.$\frac {7}{8}$
答案:
D
7. (多选题)大数据时代为媒体带来了前所未有的丰富数据资源和先进的数据科学技术,在AI算法的驱动下,无论是编辑图文、视频,还是素材制作,所有的优质内容创作都变得更加容易.已知某数据库有视频a个,图片b张$(a,b\in \mathbf{N}且a>b>1)$.从中随机选出一个视频和一张图片,记“视频甲和图片乙入选”为事件A,“视频甲入选”为事件B,“图片乙入选”为事件C,则下列判断中正确的是 (
A.$P(A)= P(B)+P(C)$
B.$P(A)= P(B)\cdot P(C)$
C.$P(\overline {A})>P(\overline {B}C)+P(B\overline {C})$
D.$P(\overline {B}C)\lt P(B\overline {C})$
BC
)A.$P(A)= P(B)+P(C)$
B.$P(A)= P(B)\cdot P(C)$
C.$P(\overline {A})>P(\overline {B}C)+P(B\overline {C})$
D.$P(\overline {B}C)\lt P(B\overline {C})$
答案:
BC 显然事件 $ B $,$ C $ 相互独立,且 $ A = BC $,于是 $ P(A)=P(B)·P(C) $,所以 A 错误,B 正确;事件 $ \overline{A} $ 包含“视频甲未入选,图片乙入选”“视频甲入选,图片乙未入选”“视频甲、图片乙都未入选”三种情况,因此 $ P(\overline{A}) = P(\overline{B}C)+P(B\overline{C})+P(\overline{B}\overline{C}) $,则 $ P(\overline{A}) > P(\overline{B}C)+P(B\overline{C}) $,所以 C 正确;依题意,$ P(\overline{B}C)=P(\overline{B})P(C)=(1 - \frac{1}{a})·\frac{1}{b}=\frac{a - 1}{ab} $,$ P(B\overline{C})=P(B)P(\overline{C}) = \frac{1}{a}·(1 - \frac{1}{b})=\frac{b - 1}{ab} $,而 $ a,b∈N $ 且 $ a > b > 1 $,因此 $ \frac{a - 1}{ab} > \frac{b - 1}{ab} $,即 $ P(\overline{B}C) > P(B\overline{C}) $,所以 D 错误。
8. (多选题)某商场推出二次开奖活动,凡购买一定价值的商品可以获得一张奖券.奖券上有一个兑奖号码,可以分别参加两次抽奖方式相同的兑奖活动.如果两次兑奖活动的中奖概率都是0.05,则两次抽奖中 (
A.都抽到某一指定号码的概率为0.05
B.都没有抽到某一指定号码的概率为0.95
C.恰有一次抽到某一指定号码的概率为0.095
D.至少有一次抽到某一指定号码的概率为0.0975
CD
)A.都抽到某一指定号码的概率为0.05
B.都没有抽到某一指定号码的概率为0.95
C.恰有一次抽到某一指定号码的概率为0.095
D.至少有一次抽到某一指定号码的概率为0.0975
答案:
CD 记“第一次抽奖抽到某一指定号码”为事件 $ A $,“第二次抽奖抽到某一指定号码”为事件 $ B $,则“两次抽奖都抽到某一指定号码”就是事件 $ AB $。由于两次抽奖结果互不影响,因此 $ A $ 与 $ B $ 相互独立。于是由独立性可得,两次抽奖都抽到某一指定号码的概率 $ P(AB)=P(A)P(B)=0.05×0.05 = 0.0025 $。同理“两次抽奖都没有抽到某一指定号码”的概率 $ P(\overline{A}\overline{B})=P(\overline{A})P(\overline{B}) = 0.95×0.95 = 0.9025 $;“两次抽奖恰有一次抽到某一指定号码”可以用 $ (A\overline{B})∪(\overline{A}B) $ 表示。由于事件 $ A\overline{B} $ 与 $ \overline{A}B $ 互斥,根据概率加法公式和相互独立事件的定义,所求的概率为 $ P(A\overline{B})+P(\overline{A}B)=P(A)P(\overline{B})+P(\overline{A})P(B)=0.05×(1 - 0.05)+(1 - 0.05)×0.05 = 0.095 $;“两次抽奖至少有一次抽到某一指定号码”可用 $ (AB)∪(A\overline{B})∪(\overline{A}B) $ 表示。由于事件 $ AB $,$ A\overline{B} $ 和 $ \overline{A}B $ 两两互斥,据概率加法公式和相互独立事件的定义,所求的概率为 $ P(AB)+P(A\overline{B})+P(\overline{A}B)=0.0025 + 0.095 = 0.0975 $。
9. 甲袋中有8个白球,4个红球,乙袋中有6个白球,6个红球,从每袋中任取一球,则取到相同颜色的球的概率是
$\frac{1}{2}$
.
答案:
$\frac{1}{2}$
10. 某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为$\frac {16}{25}$,则该队员每次罚球的命中率为
$\frac{3}{5}$
.
答案:
$\frac{3}{5}$
11. 事件A,B,C相互独立,如果$P(AB)= \frac {1}{6}$,$P(\overline {B}C)= \frac {1}{8}$,$P(AB\overline {C})= \frac {1}{8}$,则$P(B)=$
$\frac{1}{2}$
,$P(\overline {A}B)=$$\frac{1}{3}$
.
答案:
$\frac{1}{2}$,$\frac{1}{3}$
查看更多完整答案,请扫码查看


