2025年暑假作业甘肃少年儿童出版社高一数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1.(多选题)如图,D,E,F分别是△ABC的边AB,BC,CA的中点,则$\overrightarrow {AF}-\overrightarrow {DB}= $ (
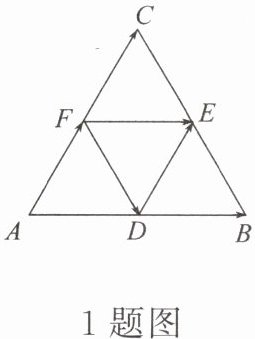
A.$\overrightarrow {FD}$
B.$\overrightarrow {EC}$
C.$\overrightarrow {BE}$
D.$\overrightarrow {DF}$
BCD
)
A.$\overrightarrow {FD}$
B.$\overrightarrow {EC}$
C.$\overrightarrow {BE}$
D.$\overrightarrow {DF}$

答案:
BCD 因为 D,E,F 分别是 $\triangle ABC$ 的边 AB,BC,CA 的中点,
所以 $DF // BE$,且 $DF = BE$,$DF // EC$,
且 $DF = EC$,所以 $\overrightarrow{DF} = \overrightarrow{BE}$,$\overrightarrow{DF} = \overrightarrow{EC}$,
所以 $\overrightarrow{AF} - \overrightarrow{DB} = \overrightarrow{AF} - \overrightarrow{AD} = \overrightarrow{DF} = \overrightarrow{BE} = \overrightarrow{EC}$。
所以 $DF // BE$,且 $DF = BE$,$DF // EC$,
且 $DF = EC$,所以 $\overrightarrow{DF} = \overrightarrow{BE}$,$\overrightarrow{DF} = \overrightarrow{EC}$,
所以 $\overrightarrow{AF} - \overrightarrow{DB} = \overrightarrow{AF} - \overrightarrow{AD} = \overrightarrow{DF} = \overrightarrow{BE} = \overrightarrow{EC}$。
2.已知下列各式:①$\overrightarrow {AM}+\overrightarrow {MB}+\overrightarrow {BA}$;②$\overrightarrow {AB}+\overrightarrow {CA}+\overrightarrow {BD}+\overrightarrow {DC}$;③$\overrightarrow {OA}+\overrightarrow {OC}+\overrightarrow {BO}+\overrightarrow {CO}$.其中结果为零向量的个数为 (
A.0
B.1
C.2
D.3
2
)A.0
B.1
C.2
D.3
答案:
C $\overrightarrow{AM} + \overrightarrow{MB} + \overrightarrow{BA} = \boldsymbol{0}$;
$\overrightarrow{AB} + \overrightarrow{CA} + \overrightarrow{BD} + \overrightarrow{DC} = \overrightarrow{AB} + \overrightarrow{BD} + \overrightarrow{DC} + \overrightarrow{CA} = \boldsymbol{0}$;$\overrightarrow{OA} + \overrightarrow{OC} + \overrightarrow{BO} + \overrightarrow{CO} = \overrightarrow{OA} + \overrightarrow{BO}$。
所以结果为零向量的个数为 2。
$\overrightarrow{AB} + \overrightarrow{CA} + \overrightarrow{BD} + \overrightarrow{DC} = \overrightarrow{AB} + \overrightarrow{BD} + \overrightarrow{DC} + \overrightarrow{CA} = \boldsymbol{0}$;$\overrightarrow{OA} + \overrightarrow{OC} + \overrightarrow{BO} + \overrightarrow{CO} = \overrightarrow{OA} + \overrightarrow{BO}$。
所以结果为零向量的个数为 2。
3.设点M是线段BC的中点,点A在直线BC外,$|\overrightarrow {BC}|^{2}= 16,|\overrightarrow {AB}+\overrightarrow {AC}|= |\overrightarrow {AB}-\overrightarrow {AC}|$,则$|\overrightarrow {AM}|= $ (
A.8
B.4
C.2
D.1
C
)A.8
B.4
C.2
D.1
答案:
C
4.设$\boldsymbol {e}_{1},\boldsymbol {e}_{2}$是两个不共线的向量,若向量$\boldsymbol {a}= 2\boldsymbol {e}_{1}-\boldsymbol {e}_{2}$,与向量$\boldsymbol {b}= \boldsymbol {e}_{1}+\lambda \boldsymbol {e}_{2}(\lambda \in \mathbf{R})$共线,则λ的值为 (
A.0
B.-1
C.-2
D.$-\frac {1}{2}$
D
)A.0
B.-1
C.-2
D.$-\frac {1}{2}$
答案:
D
5.在△ABC中,点D在边AB上,$BD= 2DA$,记$\overrightarrow {CA}= \boldsymbol {m},\overrightarrow {CD}= \boldsymbol {n}$,则$\overrightarrow {CB}= $ (
A.$3\boldsymbol {m}-2\boldsymbol {n}$
B.$-2\boldsymbol {m}+3\boldsymbol {n}$
C.$3\boldsymbol {m}+2\boldsymbol {n}$
D.$2\boldsymbol {m}+3\boldsymbol {n}$
B
)A.$3\boldsymbol {m}-2\boldsymbol {n}$
B.$-2\boldsymbol {m}+3\boldsymbol {n}$
C.$3\boldsymbol {m}+2\boldsymbol {n}$
D.$2\boldsymbol {m}+3\boldsymbol {n}$
答案:
B
6.在△ABC中,若$\overrightarrow {AB}\cdot \overrightarrow {BC}+\overrightarrow {AB}^{2}= 0$,则$\overrightarrow {BC}在\overrightarrow {BA}$上的投影向量为 (
A.$\overrightarrow {BA}$
B.$\frac {1}{2}\overrightarrow {AB}$
C.$\overrightarrow {AC}$
D.$\frac {1}{2}\overrightarrow {CA}$
$\overrightarrow{BA}$
)A.$\overrightarrow {BA}$
B.$\frac {1}{2}\overrightarrow {AB}$
C.$\overrightarrow {AC}$
D.$\frac {1}{2}\overrightarrow {CA}$
答案:
A 因为 $0 = \overrightarrow{AB} \cdot \overrightarrow{BC} + \overrightarrow{AB}^2 = \overrightarrow{AB} \cdot (\overrightarrow{BC} + \overrightarrow{AB}) = \overrightarrow{AB} \cdot \overrightarrow{AC}$,所以 $\overrightarrow{AB} \perp \overrightarrow{AC}$,
又 $\overrightarrow{BC}$ 与 $\overrightarrow{BA}$ 的夹角为锐角,所以 $\overrightarrow{BC}$ 在 $\overrightarrow{BA}$ 上的投影向量为 $\overrightarrow{BA}$。
又 $\overrightarrow{BC}$ 与 $\overrightarrow{BA}$ 的夹角为锐角,所以 $\overrightarrow{BC}$ 在 $\overrightarrow{BA}$ 上的投影向量为 $\overrightarrow{BA}$。
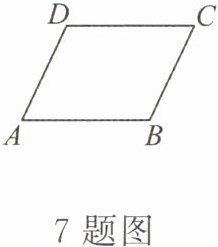
7.(多选题)在平行四边形ABCD中,下列结论正确的是 (
A.$\overrightarrow {AB}= \overrightarrow {DC}$
B.$\overrightarrow {AC}= \overrightarrow {AB}+\overrightarrow {AD}$
C.$\overrightarrow {BD}= \overrightarrow {AB}+\overrightarrow {AD}$
D.$\overrightarrow {AD}+\overrightarrow {CB}= \boldsymbol {0}$
ABD
)
A.$\overrightarrow {AB}= \overrightarrow {DC}$
B.$\overrightarrow {AC}= \overrightarrow {AB}+\overrightarrow {AD}$
C.$\overrightarrow {BD}= \overrightarrow {AB}+\overrightarrow {AD}$
D.$\overrightarrow {AD}+\overrightarrow {CB}= \boldsymbol {0}$
答案:
ABD
8.(多选题)设向量$\boldsymbol {a},\boldsymbol {b}$满足$|\boldsymbol {a}|= |\boldsymbol {b}|= 1$,且$|\boldsymbol {b}-2\boldsymbol {a}|= \sqrt {5}$,则以下结论正确的是 (
A.$\boldsymbol {a}\perp \boldsymbol {b}$
B.$|\boldsymbol {a}+\boldsymbol {b}|= 2$
C.$|\boldsymbol {a}-\boldsymbol {b}|= \sqrt {2}$
D.$\langle \boldsymbol {a},\boldsymbol {b}\rangle =60^{\circ }$
AC
)A.$\boldsymbol {a}\perp \boldsymbol {b}$
B.$|\boldsymbol {a}+\boldsymbol {b}|= 2$
C.$|\boldsymbol {a}-\boldsymbol {b}|= \sqrt {2}$
D.$\langle \boldsymbol {a},\boldsymbol {b}\rangle =60^{\circ }$
答案:
AC $|a| = |b| = 1$,且 $|b - 2a| = \sqrt{5}$,平方得 $b^2 + 4a^2 - 4a \cdot b = 5$,即 $a \cdot b = 0$,
可得 $a \perp b$,$\langle a, b \rangle = 90^\circ$,A 正确,D 错误;$(a + b)^2 = a^2 + b^2 + 2a \cdot b = 2$,可得 $|a + b| = \sqrt{2}$,B 错误;$(a - b)^2 = a^2 + b^2 - 2a \cdot b = 2$,可得 $|a - b| = \sqrt{2}$,C 正确。
可得 $a \perp b$,$\langle a, b \rangle = 90^\circ$,A 正确,D 错误;$(a + b)^2 = a^2 + b^2 + 2a \cdot b = 2$,可得 $|a + b| = \sqrt{2}$,B 错误;$(a - b)^2 = a^2 + b^2 - 2a \cdot b = 2$,可得 $|a - b| = \sqrt{2}$,C 正确。
9.设向量$\boldsymbol {a},\boldsymbol {b}的夹角的余弦值为\frac {1}{3}$,且$|\boldsymbol {a}|= 1$,$|\boldsymbol {b}|= 3$,则$(2\boldsymbol {a}+\boldsymbol {b})\cdot \boldsymbol {b}= $
11
.
答案:
【解析】由题意可得 $a \cdot b = 1 × 3 × \frac{1}{3} = 1$,$b^2 = 9$,则 $(2a + b) \cdot b = 2a \cdot b + b^2 = 2 + 9 = 11$。
答案:11
答案:11
10.已知向量$\boldsymbol {a},\boldsymbol {b}的夹角为45^{\circ }$,且$|\boldsymbol {a}|= 4$,$(\frac {1}{2}\boldsymbol {a}+\boldsymbol {b})\cdot (2\boldsymbol {a}-3\boldsymbol {b})= 12$,则$|\boldsymbol {b}|= $
$\sqrt{2}$
,$\boldsymbol {b}在\boldsymbol {a}$方向上的投影等于______.
答案:
$\sqrt{2}$
11.已知$|\boldsymbol {a}|= 1,|\boldsymbol {b}|= 2,\boldsymbol {a}与\boldsymbol {b}的夹角为60^{\circ },\boldsymbol {c}= \lambda \boldsymbol {a}+\boldsymbol {b}与\boldsymbol {d}= \boldsymbol {a}+2\boldsymbol {b}$的夹角为锐角,则λ的取值范围为
$\left\{ \lambda \left| \lambda > -3 \text{ 且 } \lambda \neq \frac{1}{2} \right. \right\}$
.
答案:
$\left\{ \lambda \left| \lambda > -3 \text{ 且 } \lambda \neq \frac{1}{2} \right. \right\}$
12.(2023·新高考Ⅱ卷)已知向量$\boldsymbol {a},\boldsymbol {b}满足|\boldsymbol {a}-\boldsymbol {b}|= \sqrt {3},|\boldsymbol {a}+\boldsymbol {b}|= |2\boldsymbol {a}-\boldsymbol {b}|$,则$|\boldsymbol {b}|= $
$\sqrt{3}$
.
答案:
【命题意图】本题考查平面向量的基本运算。
【解析】由 $|a + b| = |2a - b|$,得 $a^2 = 2a \cdot b$;由 $|a - b| = \sqrt{3}$,得 $a^2 - 2a \cdot b + b^2 = 3$,即 $b^2 = 3$,$|b| = \sqrt{3}$。
答案:$\sqrt{3}$
【解析】由 $|a + b| = |2a - b|$,得 $a^2 = 2a \cdot b$;由 $|a - b| = \sqrt{3}$,得 $a^2 - 2a \cdot b + b^2 = 3$,即 $b^2 = 3$,$|b| = \sqrt{3}$。
答案:$\sqrt{3}$
13.已知向量$\overrightarrow {AB}= \boldsymbol {a}+5\boldsymbol {b},\overrightarrow {BC}= -2\boldsymbol {a}+8\boldsymbol {b},\overrightarrow {CD}= 3(\boldsymbol {a}-\boldsymbol {b})$,
(1)求证:A,B,D三点共线;
(2)求证:$\overrightarrow {CA}= x\overrightarrow {CB}+y\overrightarrow {CD}$(其中$x+y= 1$).
(1)求证:A,B,D三点共线;
(2)求证:$\overrightarrow {CA}= x\overrightarrow {CB}+y\overrightarrow {CD}$(其中$x+y= 1$).
答案:
【证明】
(1) 因为 $\overrightarrow{BD} = \overrightarrow{BC} + \overrightarrow{CD} = -2a + 8b + 3(a - b) = a + 5b$,$\overrightarrow{AB} = a + 5b$,
所以 $\overrightarrow{AB} = \overrightarrow{BD}$,所以 $\overrightarrow{AB} // \overrightarrow{BD}$,
又 $\overrightarrow{AB}$,$\overrightarrow{BD}$ 有公共点 B,所以 A,B,D 三点共线。
(2) 因为 $\overrightarrow{CA} = \overrightarrow{CB} + \overrightarrow{BA} = -\overrightarrow{BC} - \overrightarrow{AB} = 2a - 8b - a - 5b = a - 13b$,
$x \overrightarrow{CB} + y \overrightarrow{CD} = x(2a - 8b) + 3y(a - b) = (2x + 3y)a + (-8x - 3y)b$,
所以 $\begin{cases} 2x + 3y = 1, \\ -8x - 3y = -13, \end{cases}$
所以 $\begin{cases} x = 2, \\ y = -1, \end{cases}$
所以 $\overrightarrow{CA} = x \overrightarrow{CB} + y \overrightarrow{CD}$,其中 $x + y = 1$。
(1) 因为 $\overrightarrow{BD} = \overrightarrow{BC} + \overrightarrow{CD} = -2a + 8b + 3(a - b) = a + 5b$,$\overrightarrow{AB} = a + 5b$,
所以 $\overrightarrow{AB} = \overrightarrow{BD}$,所以 $\overrightarrow{AB} // \overrightarrow{BD}$,
又 $\overrightarrow{AB}$,$\overrightarrow{BD}$ 有公共点 B,所以 A,B,D 三点共线。
(2) 因为 $\overrightarrow{CA} = \overrightarrow{CB} + \overrightarrow{BA} = -\overrightarrow{BC} - \overrightarrow{AB} = 2a - 8b - a - 5b = a - 13b$,
$x \overrightarrow{CB} + y \overrightarrow{CD} = x(2a - 8b) + 3y(a - b) = (2x + 3y)a + (-8x - 3y)b$,
所以 $\begin{cases} 2x + 3y = 1, \\ -8x - 3y = -13, \end{cases}$
所以 $\begin{cases} x = 2, \\ y = -1, \end{cases}$
所以 $\overrightarrow{CA} = x \overrightarrow{CB} + y \overrightarrow{CD}$,其中 $x + y = 1$。
查看更多完整答案,请扫码查看


