2025年暑假作业甘肃少年儿童出版社高一数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业甘肃少年儿童出版社高一数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. $(\overrightarrow {AB}+\overrightarrow {MB})+(\overrightarrow {BO}+\overrightarrow {BC})+\overrightarrow {OM}$化简后等于 (
A.$\overrightarrow {BC}$
B.$\overrightarrow {AB}$
C.$\overrightarrow {AC}$
D.$\overrightarrow {AM}$
C
)A.$\overrightarrow {BC}$
B.$\overrightarrow {AB}$
C.$\overrightarrow {AC}$
D.$\overrightarrow {AM}$
答案:
C 原式$=\overrightarrow {AB}+\overrightarrow {BO}+\overrightarrow {OM}+\overrightarrow {MB}+\overrightarrow {BC}=\overrightarrow {AC}.$
2. 在$\triangle ABC$中,$A= 60^{\circ },B= 75^{\circ },a= 10$,则c等于 (
A.$5\sqrt {2}$
B.$10\sqrt {2}$
C.$\frac {10\sqrt {6}}{3}$
D.$5\sqrt {6}$
C
)A.$5\sqrt {2}$
B.$10\sqrt {2}$
C.$\frac {10\sqrt {6}}{3}$
D.$5\sqrt {6}$
答案:
C
3. 设$x,y∈R$,向量$\boldsymbol{a}= (x,1),\boldsymbol{b}= (1,y),\boldsymbol{c}= (2,-4)$,且$\boldsymbol{a}⊥\boldsymbol{c},\boldsymbol{b}// \boldsymbol{c}$,则$|\boldsymbol{a}+\boldsymbol{b}|= $ (
A.$\sqrt {5}$
B.$\sqrt {10}$
C.$2\sqrt {5}$
D.10
B
)A.$\sqrt {5}$
B.$\sqrt {10}$
C.$2\sqrt {5}$
D.10
答案:
B
4. 如图所示,在正方形 ABCD 中,E 为 AB 的中点,F 为 CE 的中点,则$\overrightarrow {AF}= $ (
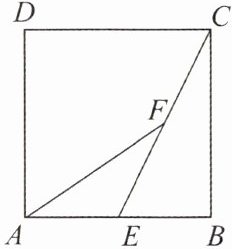
A.$\frac {3}{4}\overrightarrow {AB}+\frac {1}{4}\overrightarrow {AD}$
B.$\frac {1}{4}\overrightarrow {AB}+\frac {3}{4}\overrightarrow {AD}$
C.$\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD}$
D.$\frac {3}{4}\overrightarrow {AB}+\frac {1}{2}\overrightarrow {AD}$
D
)
A.$\frac {3}{4}\overrightarrow {AB}+\frac {1}{4}\overrightarrow {AD}$
B.$\frac {1}{4}\overrightarrow {AB}+\frac {3}{4}\overrightarrow {AD}$
C.$\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD}$
D.$\frac {3}{4}\overrightarrow {AB}+\frac {1}{2}\overrightarrow {AD}$
答案:
D
5. 在$\triangle ABC$中,a,b,c分别为角A,B,C的对边,若$B= 45^{\circ },C= 60^{\circ },c= 1$,则最短边长为(
A.$\frac {\sqrt {6}}{2}$
B.$\frac {\sqrt {6}}{3}$
C.$\frac {1}{2}$
D.$\frac {\sqrt {3}}{2}$
$\frac{\sqrt{6}}{3}$
)A.$\frac {\sqrt {6}}{2}$
B.$\frac {\sqrt {6}}{3}$
C.$\frac {1}{2}$
D.$\frac {\sqrt {3}}{2}$
答案:
B $A=180^{\circ }-(60^{\circ }+45^{\circ })=75^{\circ },$故最短边为b,由正弦定理可得$\frac {b}{sinB}=\frac {c}{sinC},$即$b=\frac {csinB}{sinC}=\frac {1×sin45^{\circ }}{sin60^{\circ }}=\frac {\sqrt {6}}{3}.$
6. 逢山开路,遇水架桥.我国摘取了一系列高速公路“世界之最”,锻造出中国路、中国桥等一张张闪亮的“中国名片”.如图,一辆汽车在一条水平的高速公路上直线行驶,在A,B,C三处测得道路一侧山顶P的仰角依次为$30^{\circ },$$45^{\circ },60^{\circ }$,其中$AB= a,BC= b(0\lt a<3b)$,则此山的高度为 (
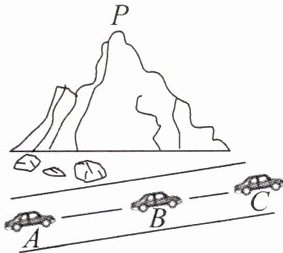
A.$\frac {1}{2}\sqrt {\frac {2ab(a+b)}{3b-a}}$
B.$\frac {1}{2}\sqrt {\frac {3ab(a+b)}{3b-a}}$
C.$\frac {1}{2}\sqrt {\frac {5ab(a+b)}{3b-a}}$
D.$\frac {1}{2}\sqrt {\frac {6ab(a+b)}{3b-a}}$
D
)
A.$\frac {1}{2}\sqrt {\frac {2ab(a+b)}{3b-a}}$
B.$\frac {1}{2}\sqrt {\frac {3ab(a+b)}{3b-a}}$
C.$\frac {1}{2}\sqrt {\frac {5ab(a+b)}{3b-a}}$
D.$\frac {1}{2}\sqrt {\frac {6ab(a+b)}{3b-a}}$
答案:
D
7. 在$\triangle ABC$中,D是边BC上一点,若$AD⊥AC,$$sin∠BAC= \frac {2\sqrt {2}}{3},AD= 3,AB= 3\sqrt {2},BD= $ (
A.$\sqrt {3}$
B.2
C.$2\sqrt {3}$
D.3
A
)A.$\sqrt {3}$
B.2
C.$2\sqrt {3}$
D.3
答案:
A
8. (2023·全国乙卷)正方形 ABCD 的边长是 2,E是 AB 的中点,则$\overrightarrow {EC}\cdot \overrightarrow {ED}= $ ( )
A.$\sqrt {5}$
B.3
C.$2\sqrt {5}$
D.5
A.$\sqrt {5}$
B.3
C.$2\sqrt {5}$
D.5
答案:
B 方法一:以$\{ \overrightarrow {AB},\overrightarrow {AD}\} $为基底向量,可知$|\overrightarrow {AB}|=|\overrightarrow {AD}|=2,\overrightarrow {AB}\cdot \overrightarrow {AD}=0,$则$\overrightarrow {EC}=\overrightarrow {EB}+\overrightarrow {BC}=\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD},\overrightarrow {ED}=\overrightarrow {EA}+\overrightarrow {AD}=-\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD},$所以$\overrightarrow {EC}\cdot \overrightarrow {ED}=(\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD})\cdot (-\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD})=-\frac {1}{4}\overrightarrow {AB}^{2}+\overrightarrow {AD}^{2}=-1+4=3;$方法二:如图,以A为坐标原点建立平面直角坐标系,
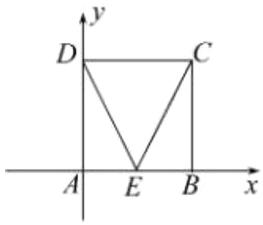
则$E(1,0),C(2,2),D(0,2)$,可得$\overrightarrow {EC}=(1,2),\overrightarrow {ED}=(-1,2),$所以$\overrightarrow {EC}\cdot \overrightarrow {ED}=-1+4=3;$方法三:由题意可得:$ED=EC=\sqrt {5},CD=2,$在$△CDE$中,由余弦定理可得$cos∠DEC=\frac {DE^{2}+CE^{2}-DC^{2}}{2DE\cdot CE}=\frac {5+5-4}{2×\sqrt {5}×\sqrt {5}}=\frac {3}{5},$所以$\overrightarrow {EC}\cdot \overrightarrow {ED}=|\overrightarrow {EC}||\overrightarrow {ED}|cos∠DEC=\sqrt {5}×\sqrt {5}×\frac {3}{5}=3.$
B 方法一:以$\{ \overrightarrow {AB},\overrightarrow {AD}\} $为基底向量,可知$|\overrightarrow {AB}|=|\overrightarrow {AD}|=2,\overrightarrow {AB}\cdot \overrightarrow {AD}=0,$则$\overrightarrow {EC}=\overrightarrow {EB}+\overrightarrow {BC}=\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD},\overrightarrow {ED}=\overrightarrow {EA}+\overrightarrow {AD}=-\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD},$所以$\overrightarrow {EC}\cdot \overrightarrow {ED}=(\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD})\cdot (-\frac {1}{2}\overrightarrow {AB}+\overrightarrow {AD})=-\frac {1}{4}\overrightarrow {AB}^{2}+\overrightarrow {AD}^{2}=-1+4=3;$方法二:如图,以A为坐标原点建立平面直角坐标系,

则$E(1,0),C(2,2),D(0,2)$,可得$\overrightarrow {EC}=(1,2),\overrightarrow {ED}=(-1,2),$所以$\overrightarrow {EC}\cdot \overrightarrow {ED}=-1+4=3;$方法三:由题意可得:$ED=EC=\sqrt {5},CD=2,$在$△CDE$中,由余弦定理可得$cos∠DEC=\frac {DE^{2}+CE^{2}-DC^{2}}{2DE\cdot CE}=\frac {5+5-4}{2×\sqrt {5}×\sqrt {5}}=\frac {3}{5},$所以$\overrightarrow {EC}\cdot \overrightarrow {ED}=|\overrightarrow {EC}||\overrightarrow {ED}|cos∠DEC=\sqrt {5}×\sqrt {5}×\frac {3}{5}=3.$
9. 已知向量$\boldsymbol{a}= (1,-2),|\boldsymbol{b}|= 4|\boldsymbol{a}|,\boldsymbol{a}// \boldsymbol{b}$,则$\boldsymbol{b}$可能是 (
A.$(4,-8)$
B.$(8,4)$
C.$(-4,-8)$
D.$(-4,8)$
AD
)A.$(4,-8)$
B.$(8,4)$
C.$(-4,-8)$
D.$(-4,8)$
答案:
AD
10. 在$\triangle ABC$中,$a= 15,b= 20,A= 30^{\circ }$,则$cosB$ $=$ (
A.$-\frac {\sqrt {5}}{3}$
B.$\frac {2}{3}$
C.$-\frac {2}{3}$
D.$\frac {\sqrt {5}}{3}$
AD
)A.$-\frac {\sqrt {5}}{3}$
B.$\frac {2}{3}$
C.$-\frac {2}{3}$
D.$\frac {\sqrt {5}}{3}$
答案:
AD
11. 对于$\triangle ABC$,如下判断正确的有 (
A.若$cosA= cosB$,则$\triangle ABC$为等腰三角形
B.若$A>B$,则$sinA>sinB$
C.若$a= 8,c= 10,B= 60^{\circ }$,则符合条件的$\triangle ABC$有两个
D.若$sin^{2}A+sin^{2}B\lt sin^{2}C$,则$\triangle ABC$是钝角三角形
ABD
)A.若$cosA= cosB$,则$\triangle ABC$为等腰三角形
B.若$A>B$,则$sinA>sinB$
C.若$a= 8,c= 10,B= 60^{\circ }$,则符合条件的$\triangle ABC$有两个
D.若$sin^{2}A+sin^{2}B\lt sin^{2}C$,则$\triangle ABC$是钝角三角形
答案:
ABD
查看更多完整答案,请扫码查看


