第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
26.(10 分)(2024·泰州泰兴期末)如图是某长方体包装盒的平面展开图,具体数据如图所示,且长方体盒子的长是高的 2 倍.
(1)展开图的 6 个面分别标有如图所示的序号,则原包装盒与①相对的面是
(2)若设长方体的高为 x cm,则:
①长方体的宽为
②求长方体包装盒的体积.
(1)展开图的 6 个面分别标有如图所示的序号,则原包装盒与①相对的面是
⑥
(填序号).(2)若设长方体的高为 x cm,则:
①长方体的宽为
$\frac{35-4x}{2}$或$\frac{20-x}{2}$
cm(用含 x 的式子表示);②求长方体包装盒的体积.
长方体的长为$2x\ \text{cm}$,高为$x\ \text{cm}$,则长方体的宽为$\frac{35-4x}{2}\ \text{cm}$或$\frac{20-x}{2}\ \text{cm}$.由题意,得$\frac{35-4x}{2}=\frac{20-x}{2}$,解得$x=5$,即长方体的长为$10\ \text{cm}$,宽为$\frac{15}{2}\ \text{cm}$,$\therefore$长方体的体积为$10×5×\frac{15}{2}=375(\text{cm}^{3})$.故这个长方体包装盒的体积为$375\ \text{cm}^{3}$.
答案:
(1)⑥ [解析]根据长方体平面展开图的“相间、Z端是对面”可知,面①与面⑥是对面.
(2)①$\frac{35-4x}{2}$或$\frac{20-x}{2}$②长方体的长为$2x\ \text{cm}$,高为$x\ \text{cm}$,则长方体的宽为$\frac{35-4x}{2}\ \text{cm}$或$\frac{20-x}{2}\ \text{cm}$.由题意,得$\frac{35-4x}{2}=\frac{20-x}{2}$,解得$x=5$,即长方体的长为$10\ \text{cm}$,宽为$\frac{15}{2}\ \text{cm}$,$\therefore$长方体的体积为$10×5×\frac{15}{2}=375(\text{cm}^{3})$.故这个长方体包装盒的体积为$375\ \text{cm}^{3}$.
(1)⑥ [解析]根据长方体平面展开图的“相间、Z端是对面”可知,面①与面⑥是对面.
(2)①$\frac{35-4x}{2}$或$\frac{20-x}{2}$②长方体的长为$2x\ \text{cm}$,高为$x\ \text{cm}$,则长方体的宽为$\frac{35-4x}{2}\ \text{cm}$或$\frac{20-x}{2}\ \text{cm}$.由题意,得$\frac{35-4x}{2}=\frac{20-x}{2}$,解得$x=5$,即长方体的长为$10\ \text{cm}$,宽为$\frac{15}{2}\ \text{cm}$,$\therefore$长方体的体积为$10×5×\frac{15}{2}=375(\text{cm}^{3})$.故这个长方体包装盒的体积为$375\ \text{cm}^{3}$.
27.(12 分) 新情境 制作长方体纸盒 (2025·福建福州期末)某“综合与实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为 24 cm 的正方形纸板制作出两种不同方案的长方体盒子(图(1)为无盖的长方体纸盒,图(2)为有盖的长方体纸盒),请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)
动手操作一:
根据图(1)方式制作一个无盖的长方体盒子.
方法:先在纸板四角剪去四个同样大小边长为 b cm 的小正方形,再沿虚线折合起来.
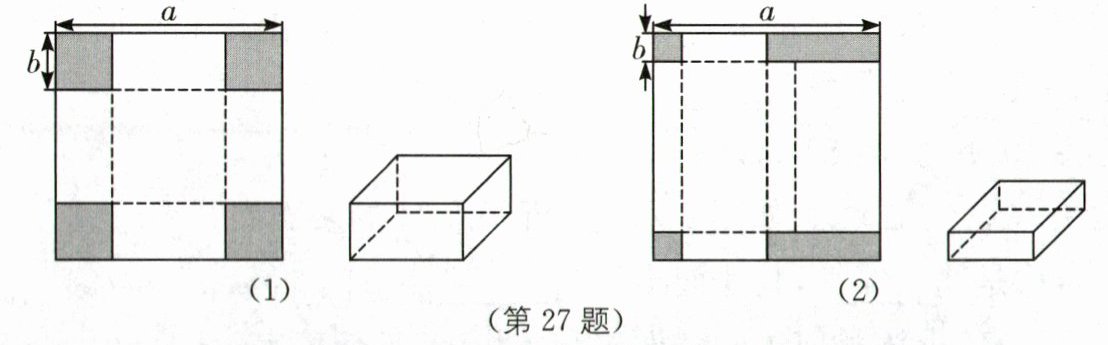
问题解决:
(1) 若$b= 6cm$,则该长方体纸盒的底面边长为______cm,该长方体纸盒的体积为______$cm^{3}$.
动手操作二:
根据图(2)方式制作一个有盖的长方体纸盒.
方法:先在纸板四角剪去两个同样大小边长为 b cm 的小正方形和两个同样大小的小长方形,再沿虚线折合起来.
拓展延伸:
(2) 若$b= 3cm$,该长方体纸盒的表面积为多少?
动手操作一:
根据图(1)方式制作一个无盖的长方体盒子.
方法:先在纸板四角剪去四个同样大小边长为 b cm 的小正方形,再沿虚线折合起来.

问题解决:
(1) 若$b= 6cm$,则该长方体纸盒的底面边长为______cm,该长方体纸盒的体积为______$cm^{3}$.
动手操作二:
根据图(2)方式制作一个有盖的长方体纸盒.
方法:先在纸板四角剪去两个同样大小边长为 b cm 的小正方形和两个同样大小的小长方形,再沿虚线折合起来.
拓展延伸:
(2) 若$b= 3cm$,该长方体纸盒的表面积为多少?
12
864
该长方体纸盒的表面积为$486\ \text{cm}^2$。
答案:
(1)12 864 [解析]该长方体纸盒的底面边长为$24-2×6=12(\text{cm})$,该长方体纸盒的体积为$12×12×6=864(\text{cm}^{3})$.
(2)裁剪后折叠成长方体的长为$a-2b=18$,裁剪后折叠成长方体的宽为$\frac{a-2b}{2}=9$,裁剪后折叠成长方体的高为3.$\therefore$长方体纸盒的表面积为$2×(18×9+9×3+18×3)=486(\text{cm}^{2})$.
(1)12 864 [解析]该长方体纸盒的底面边长为$24-2×6=12(\text{cm})$,该长方体纸盒的体积为$12×12×6=864(\text{cm}^{3})$.
(2)裁剪后折叠成长方体的长为$a-2b=18$,裁剪后折叠成长方体的宽为$\frac{a-2b}{2}=9$,裁剪后折叠成长方体的高为3.$\therefore$长方体纸盒的表面积为$2×(18×9+9×3+18×3)=486(\text{cm}^{2})$.
查看更多完整答案,请扫码查看


