《2025年实验班提优大考卷七年级数学上册苏科版江苏专用》

24. (9 分)作图和说理.
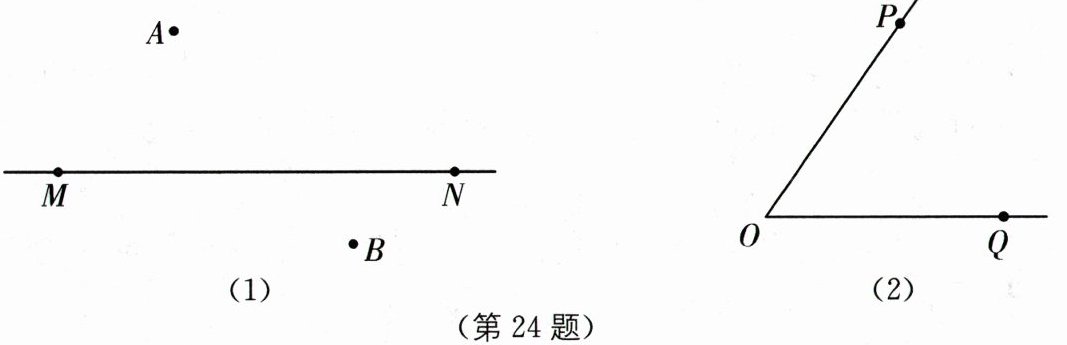
(1)如图(1),在公路$MN的两侧各有一所学校A$,$B$,一辆拖拉机沿着$MN$(从$M到N$)方向行驶.
①请在公路$MN上作一点C$,使得拖拉机行驶到该点时在学校$A$听到的拖拉机噪声最大;在公路$MN上作一点D$,使得拖拉机行驶到该点时在学校$B$听到的拖拉机噪声最大.
你的依据是______;
②在公路$MN$上的______段,随着拖拉机的行驶,在学校$A$听到的拖拉机噪声越来越小,而在学校$B$听到的拖拉机噪声越来越大;
(2)如图(2),已知$\angle POQ$.
①利用无刻度的直尺和圆规,在射线$OQ的下方作\angle OQR$,使得$\angle OQR= \angle POQ$(不写作法保留作图痕迹);
②$OP与QR$的位置关系是______,理由是:______.

答案：
[解析]本题考查作图——应用与设计作图，解题的关键是理解题意，灵活运用所学知识解决问题。
解：
(1)①垂线段最短 提示：如图
(1)中，点 C，D 即为所求，作图依据是垂线段最短。
　
②CD
(2)①图形如图
(2)所示。
②$OP// QR$ 内错角相等，两直线平行。

25. (9 分)甲乙两地相距$600km$,一辆客车从甲地开往乙地,速度为$60km/h$,一辆出租车从乙地开往甲地,速度为$100km/h$,两车同时出发,到达各自目的地后停止行驶. 设客车行驶时间为$t h$.
(1)出发多长时间两车相遇?
(2)分别写出$t = 3$,$t = 5和t = 8$时两车的距离.
(3)甲,乙两地之间有$A$,$B$两个加油站,相距$200km$,若客车进入$A$站加油时,出租车恰好进入$B$站加油. 求$A$加油站到甲地的距离.

答案： [解析]本题考查一元一次方程的应用，解题的关键是读懂题意，找到等量关系列出方程。
解：
(1)根据题意，得$60t + 100t = 600$，解得$t = \frac{15}{4}$，
∴出发$\frac{15}{4}$小时两车相遇。
(2)当$t = 3$时，两车相距$600 - 3×(60 + 100) = 120(km)$；
当$t = 5$时，两车相距$5×(60 + 100) - 600 = 200(km)$；
当$t = 8$时，乙车已经到达目的地，此时两车相距$8×60 = 480(km)$。
(3)设 A 加油站到甲地的距离为 x km，
当 A 加油站比 B 加油站更靠近甲地时，
$\frac{x}{60} = \frac{600 - 200 - x}{100}$，解得$x = 150$；
当 A 加油站比 B 加油站更靠近乙地时，
$\frac{x}{60} = \frac{600 - x + 200}{100}$，解得$x = 300$。
故 A 加油站到甲地的距离为 150 km 或 300 km。