《2025年实验班提优大考卷七年级数学上册苏科版江苏专用》

1. -2025 的相反数是(C).
A.-2025
B.$-\frac{1}{2025}$
C.2025
D.$\frac{1}{2025}$

答案： C

2. 下列运算中,正确的是(D).
A.$2a + a = 2a^2$
B.$2a + 3b = 5ab$
C.$5y^2 - 3y^2 = 2$
D.$3ab^2 - 2ab^2 = ab^2$

答案： D [解析]本题考查了合并同类项，根据合并同类项的计算法则逐项计算判断即可。
A. 2a + a = 3a，原计算错误，不符合题意；B. 2a 与 3b 不是同类项，不能合并，不符合题意；C. 5y² - 3y² = 2y²，原计算错误，不符合题意；D. 3ab² - 2ab² = ab²，计算正确，符合题意。故选 D。
知识拓展 同类项定义中的两个“相同”：①所含字母相同；②相同字母的指数相同。注意常数项也是同类项，同类项定义中的两个“无关”：①与字母的顺序无关；②与系数无关。

3. 下列等式变形中,错误的是(C).
A.若$a + 4 = b + 4$,则$a = b$
B.若$a = b$,则$-a = -b$
C.若$ac = bc$,则$a = b$
D.若$a = b$,则$\frac{a}{2} = \frac{b}{2}$

答案： C [解析]本题考查了等式的性质。根据等式的性质对各个选项进行判断即可。
A. 若 a + 4 = b + 4，等式两边同时减去 4，则 a + 4 - 4 = b + 4 - 4，即 a = b，故选项 A 正确，不符合题意；B. 若 a = b，等式两边同时乘以 -1，得 -a = -b，故选项 B 正确，不符合题意；C. 若 ac = bc，等式两边同时除以 c（c≠0），则 a = b，故选项 C 错误，符合题意；D. 若 a = b，等式两边同时除以 2，得$\frac{a}{2}=\frac{b}{2}$，故选项 D 正确，不符合题意。故选 C。
知识拓展 等式的基本性质：等式的基本性质 1 是等式的两边都加上（或减去）同一个整式，所得的结果仍是等式；等式的基本性质 2 是等式的两边都乘（或除以）同一个数（除数不能为 0），所得的结果仍是等式。

4. 为贯彻落实党中央国务院关于促消费和惠民生有关要求,进一步提振消费,江苏省有关部门发布了相关数码产品补贴专项活动. 从 2024 年 11 月 27 日至 12 月 31 日,凡购买手机、平板电脑、智能手表等数码产品,可享受 15%的补贴,即优惠 15%. 若标价为$a$元的某品牌手机参与本次补贴专项活动,则顾客购买一部此品牌手机实际支付的费用为(B).
A.$(1 + 15\%)a$元
B.$(1 - 15\%)a$元
C.$\frac{a}{1 + 15\%}$元
D.$\frac{a}{1 - 15\%}$元

答案： B

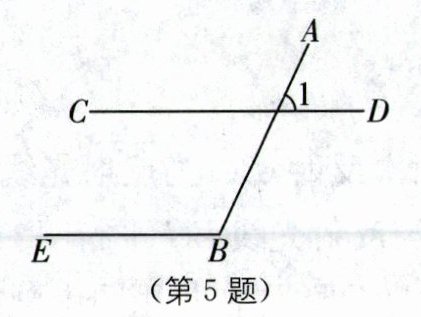
5. 如图,若$CD // EB$,$\angle 1 = 65^{\circ}$,则$\angle B$的度数是( ).

A.$115^{\circ}$
B.$110^{\circ}$
C.$105^{\circ}$
D.$65^{\circ}$
]

答案：
A [解析]本题考查平行线性质。根据对顶角性质和平行线性质可得。
如图，
∵∠1 = 65°，
∴∠2 = 65°。
∵CD//EB，
∴∠B + ∠2 = 180°，
→两直线平行，同旁内角互补
∴∠B = 180° - 65° = 115°。故选 A。

一题多解 如图，
∵∠1 = 65°，
∴∠2 = 115°。
∵CD//EB，
∴∠B = ∠2 = 115°。故选 A。

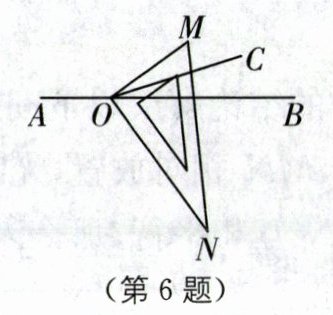
6. 如图,$O是直线AB$上一点,将直角三角板的直角顶点放在点$O$处(点$M$,$N分别在AB$异侧),射线$OC平分\angle BOM$. 若$\angle AOC = 3\angle BON$,则$\angle AOM$的度数为( ).

A.$110^{\circ}$
B.$120^{\circ}$
C.$135^{\circ}$
D.$144^{\circ}$
]

答案： D [解析]本题考查角平分线的定义，余角和补角。设∠BOC = x，根据∠AOC = 3∠BON，列方程即可得到结论。
设∠BOC = x，则∠COM = x，∠AOM = 180° - 2x，∠BON = 90° - 2x，
∴∠AOC = (180° - 2x) + x = 180° - x。
∵∠AOC = 3∠BON，
∴180° - x = 3(90° - 2x)，解得 x = 18°。
∴∠AOM = 180° - 2×18° = 144°。故选 D。
知识拓展 余角和补角的定义：①如果两个角的和等于 90°，那么这两个角互为余角，其中一个角叫作另一个角的余角；②如果两个角的和等于 180°，那么这两个角互为补角，其中一个角叫作另一个角的补角。

7. 《九章算术》被誉为人类科学史上应用数学的“算经之首”,其中有一题为“今有甲发长安,五日至齐;乙发齐,七日至长安. 今乙发已先二日,甲乃发长安. 问几何日相逢?”其大意如下:甲从长安出发,用 5 天时间可到达齐国;乙从齐国出发,用 7 天时间可到达长安. 若乙先从齐国出发 2 天,甲才从长安出发,问甲经过多少天与乙相遇? 设甲经过$x$天后与乙相遇,则下列方程正确的是(D).
A.$\frac{1}{5}x + \frac{1}{7}x = 1$
B.$\frac{1}{5}x - \frac{1}{7}x = 1$
C.$\frac{1}{5}(x + 2) + \frac{1}{7}x = 1$
D.$\frac{1}{5}x + \frac{1}{7}(x + 2) = 1$

答案： D

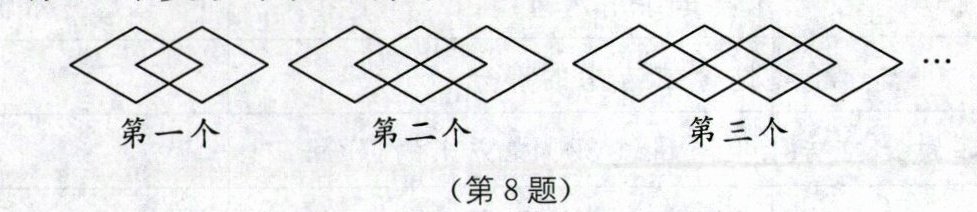
8. 方胜纹是以几个菱形压角相叠而构成的几何图形(注:四条边都相等的四边形是菱形),是中国传统吉祥装饰纹样中一种独具特色的几何纹样. 苏州拙政园远香堂方形窗棂上就装饰有这种纹样. 如图,第一个图案中有 3 个菱形,第二个图案中有 7 个菱形,第三个图案中有 11 个菱形,…,按照这样的方法排列下去,若第$n$个图案中有 43 个菱形,则$n$的值是(C).

A.9
B.10
C.11
D.12
]

答案： C [解析]本题考查了图形变化规律。根据所给图形，依次求出图形中菱形的个数，发现规律即可解决问题。
由所给图形可知，第 1 个图案中菱形的个数为 3 = 1×4 - 1；第 2 个图案中菱形的个数为 7 = 2×4 - 1；第 3 个图案中菱形的个数为 11 = 3×4 - 1；…；所以第 n 个图案中菱形的个数为(4n - 1)个。令 4n - 1 = 43，解得 n = 11，即第 11 个图案中菱形有 43 个。故选 C。
方法诠释 规律型——图形的变化类，解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，有的需要从循环的角度入手，找出数量上的变化规律，从而推出一般性的结论。