《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

22. 如图,在$\triangle ABC$中,$CD$是高,$AD = 4$,$CD = 2$,$BD = 1$,求证：$\angle ACB = 90^{\circ}$。

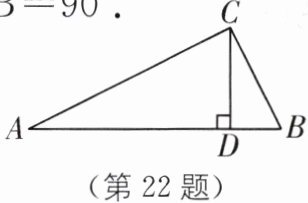
答案： $\because CD$是$\triangle ABC$的高，$\therefore \angle ADC=\angle BDC = 90^{\circ}$。$\because AD = 4$，$CD = 2$，$BD = 1$，$\therefore AC^{2}=AD^{2}+CD^{2}=4^{2}+2^{2}=20$，$BC^{2}=BD^{2}+CD^{2}=1^{2}+2^{2}=5$，$AB = AD + BD = 4 + 1 = 5$。$\therefore AC^{2}+BC^{2}=AB^{2}$。$\therefore \triangle ABC$是直角三角形，且$\angle ACB = 90^{\circ}$。方法诠释：本题主要考查了勾股定理的逆定理：如果三角形的三边长$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$，那么这个三角形就是直角三角形。

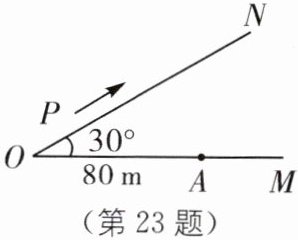
23. 如图,有两条公路$OM$、$ON相交成30^{\circ}$角,沿公路$OM方向离点O80米处有一所学校A$。当重型运输卡车$P沿道路ON$方向行驶时,在以$P$为圆心、$50$米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车$P与学校A$的距离越近噪声影响越大。若已知重型运输卡车$P沿道路ON方向行驶的速度为18$千米/小时。
(1)求对学校$A的噪声影响最大时卡车P与学校A$的距离；
(2)求卡车$P沿道路ON方向行驶一次给学校A$带来噪声影响的时间。

答案：

(1)过点$A$作$AD\perp ON$于点$D$。$\because \angle NOM = 30^{\circ}$，$AO = 80m$，$\therefore AD = 40m$。即对学校$A$的噪声影响最大时卡车$P$与学校$A$的距离为40米。
(2)由图可知，在点$A$处以$50m$为半径画圆，分别交$ON$于$B$、$C$两点，$AD\perp BC$，$BD = CD=\frac{1}{2}BC$，$OA = 80m$，$\because$在$Rt\triangle AOD$中，$\angle AOB = 30^{\circ}$，$\therefore AD=\frac{1}{2}OA=\frac{1}{2}×80 = 40(m)$。在$Rt\triangle ABD$中，$AB = 50m$，$AD = 40m$，由勾股定理，得$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{50^{2}-40^{2}}=30(m)$。故$BC = 2×30 = 60(m)$，即重型运输卡车在经过$BC$时对学校产生影响。$\because$重型运输卡车的速度为18千米/小时，即$\frac{18000}{60}=300$米/分钟，$\therefore$重型运输卡车经过$BC$时需要$60÷300 = 0.2$(分钟)$ = 12$(秒)。故卡车$P$沿道路$ON$方向行驶一次给学校$A$带来噪声影响的时间为12秒。

24. 如图,一根长$2.5m的木棍(AB)$,斜靠在与地面$(OM)垂直的墙(ON)$上,此时$OB的距离为0.7m$,设木棍的中点为$P$。木棍$A$端沿墙下滑,且$B$端沿地面向右滑行。
(1)如果木棍的顶端$A沿墙下滑0.4m$,那么木棍的底端$B$向外移动多少距离？
(2)请判断木棍滑动的过程中,点$P到点O$的距离是否变化,并简述理由。
(3)在木棍滑动的过程中,当滑动到什么位置时,$\triangle AOB$的面积最大？简述理由,并求出面积的最大值。

答案：

(1)如图
(1)，设木棍$A$端沿墙下滑$0.4m$到达点$C$，同时$B$端沿地面向右滑行到点$D$，在$Rt\triangle ABO$中，已知$AB = 2.5m$，$BO = 0.7m$，则$AO^{2}=2.5^{2}-0.7^{2}=5.76 = 2.4^{2}$，即$AO = 2.4m$。$\because AO = AC + OC$，$\therefore OC = 2m$。$\because$在$Rt\triangle CDO$中，$AB = CD$，且$CD$为斜边，$\therefore OD^{2}=CD^{2}-OC^{2}=2.25$，即$OD = 1.5m$。$\therefore BD = OD - OB = 1.5 - 0.7 = 0.8(m)$。故木棍的底端$B$向外移动$0.8m$。
(2)不变。理由：在直角三角形中，斜边上的中线等于斜边的一半，因为斜边$AB$不变，所以斜边上的中线$OP$不变。
(3)当$\triangle AOB$的斜边上的高$h$等于中线$OP$时，面积最大。如图
(2)，若$h$与$OP$不相等，则总有$h\lt OP$，故根据三角形面积公式，当$h$与$OP$相等时，$\triangle AOB$的面积最大，此时$S_{\triangle AOB}=\frac{1}{2}AB\cdot h=\frac{1}{2}×2.5×1.25 = 1.5625$。所以$\triangle AOB$的最大面积为$1.5625m^{2}$。