《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

9. 已知反比例函数$y= \frac{k}{x}(k\neq 0)与一次函数y= x$的图像有交点,则$k$的取值范围是$k＞0$。

答案： $k＞0$

10. 中考新考法 满足条件的结论开放 如图,直线$MN:y= kx+2交x轴负半轴于点A$,交$y轴于点B$,$\angle BAO= 30^{\circ}$,点$C是x$轴上的一点,且$OC= 2$,则$\angle MBC$的度数为$75^{\circ}$或$165^{\circ}$。

答案： $75^{\circ}$或$165^{\circ}$

11. 如图,$\triangle AOB$为等边三角形,点$B的坐标为(-4,0)$,过点$C(4,0)作直线l交AO于点D$,交$AB于点E$,点$E$在某反比例函数图像上,当$\triangle ADE和\triangle DCO$的面积相等时,该反比例函数的解析式为$y=-\frac {3\sqrt {3}}{x}$。

答案： $y=-\frac {3\sqrt {3}}{x}$

12. 中考新考法 归纳一般结论 如图,在函数$y= \frac{8}{x}(x＞0)的图像上有点P_{1}$、$P_{2}$、$P_{3}$、…、$P_{n}$、$P_{n+1}$,点$P_{1}$的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点$P_{1}$、$P_{2}$、$P_{3}$、…、$P_{n}$、$P_{n+1}分别作x$轴、$y$轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为$S_{1}$、$S_{2}$、$S_{3}$、…、$S_{n}$,则$S_{n}= $$\frac {8}{n(n+1)}$。(用含$n$的代数式表示)

答案： $\frac {8}{n(n+1)}$

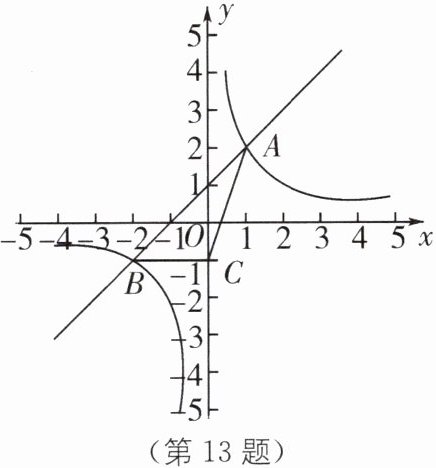
13. 如图,反比例函数$y= \frac{k}{x}的图像与一次函数y= x+b的图像交于A$、$B$两点,点$A和点B$的横坐标分别为1和$-2$,这两点的纵坐标之和为1。
(1)求反比例函数的表达式与一次函数的表达式；
(2)当点$C的坐标为(0,-1)$时,求$\triangle ABC$的面积。

答案：
(1)由题意，得1+b+(-2)+b=1，解得b=1，则一次函数的解析式为$y=x+1$，当$x=1$时，$y=x+1=2$，即$A(1,2)$，将点$A$的坐标代入$y=\frac {k}{x}$，得$k=2$，则反比例函数的解析式为$y=\frac {2}{x}$．
(2)当$x=-2$时，$y=-1$，即$B(-2,-1)$．则$BC=2$，$S_{\triangle ABC}=\frac {1}{2}BC\cdot (y_{A}-y_{C})=3$．

14. 已知$A$、$B$两地相距240km,一辆货车从$A前往B$地,途中因装载货物停留一段时间。一辆轿车沿同一条公路从$B地前往A$地,到达$A$地后(在$A$地停留时间不计)立即原路原速返回。如图是两车距$B地的距离y(km)与货车行驶时间x(h)$之间的函数图像,结合图像回答下列问题：
(1)图中$m$的值是5；轿车的速度是120km/h。
(2)求货车从$A地前往B$地的过程中,货车距$B地的距离y(km)与行驶时间x(h)$之间的函数关系式。
$y=\left\{\begin{array}{l} -66x+240(0≤x＜2.5),\\ 75(2.5≤x＜3.5),\\ -50x+250(3.5≤x≤5).\end{array}\right.$
(3)直接写出轿车从$B地到A$地行驶过程中,轿车出发多长时间与货车相距12km？
1h或$\frac {27}{31}$h

答案：
(1)5 120 [解析]由图像得$m=1+(3-1)×2=5$，轿车的速度为$240÷2=120(km/h)$．
(2)设$y_{MN}=k_{1}x+b_{1}(k_{1}≠0)(0≤x＜2.5)$，
∵图像经过点$M(0,240)$和点$N(2.5,75)$，$\therefore \left\{\begin{array}{l} b_{1}=240,\\ 2.5k_{1}+b_{1}=75,\end{array}\right. $解得$\left\{\begin{array}{l} k_{1}=-66,\\ b_{1}=240.\end{array}\right. $$\therefore y_{MN}=-66x+240(0≤x＜2.5)$．$y_{NG}=75(2.5≤x＜3.5)$；设$y_{GH}=k_{2}x+b_{2}(k_{2}≠0)(3.5≤x≤5)$，
∵图像经过点$G(3.5,75)$和点$H(5,0)$，$\therefore \left\{\begin{array}{l} 5k_{2}+b_{2}=0,\\ 3.5k_{2}+b_{2}=75,\end{array}\right. $解得$\left\{\begin{array}{l} k_{2}=-50,\\ b_{2}=250.\end{array}\right. $$\therefore y_{GH}=-50x+250$．$\therefore y=\left\{\begin{array}{l} -66x+240(0≤x＜2.5),\\ 75(2.5≤x＜3.5),\\ -50x+250(3.5≤x≤5).\end{array}\right. $
(3)货车从$A$地前往$B$地的速度为$(240-75)÷2.5=66(km/h)$．设轿车出发$a$h与货车相距12km，根据题意，得$66(1+a)+120a=240+12$或$66(1+a)+120a=240-12$，解得$a=1$或$a=\frac {27}{31}$．经检验，符合题意．故轿车从$B$地到$A$地行驶过程中，轿车出发1h或$\frac {27}{31}$h与货车相距12km．