第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 若阿光以四种不同的方式连接正六边形 $ ABCDEF $ 的两条对角线,连接后的情形如下列选项中的图形所示,则下列图形(

D
)不是轴对称图形.
答案:
D
2. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是(
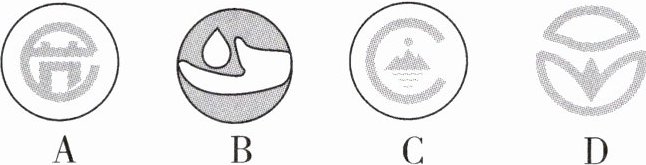
D
).
答案:
D
3. 如图是一个风筝的图案,它是以直线 $ AF $ 为对称轴的轴对称图形.下列结论中,不一定成立的是(
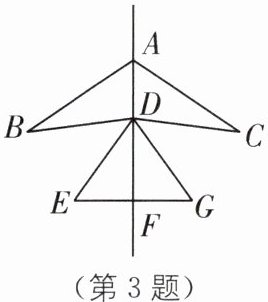
A.$ \triangle ABD \cong \triangle ACD $
B.$ AF $ 垂直平分 $ EG $
C.直线 $ BG $、$ CE $ 的交点在 $ AF $ 上
D.$ \triangle DEG $ 是等边三角形
D
).
A.$ \triangle ABD \cong \triangle ACD $
B.$ AF $ 垂直平分 $ EG $
C.直线 $ BG $、$ CE $ 的交点在 $ AF $ 上
D.$ \triangle DEG $ 是等边三角形
答案:
D
4. 等腰三角形的周长为 $ 13 \mathrm{cm} $,其中一边长为 $ 3 \mathrm{cm} $,则该等腰三角形的底边长为(
A.$ 7 \mathrm{cm} $
B.$ 3 \mathrm{cm} $
C.$ 7 \mathrm{cm} $ 或 $ 3 \mathrm{cm} $
D.$ 5 \mathrm{cm} $
B
).A.$ 7 \mathrm{cm} $
B.$ 3 \mathrm{cm} $
C.$ 7 \mathrm{cm} $ 或 $ 3 \mathrm{cm} $
D.$ 5 \mathrm{cm} $
答案:
B
5. 如图,在四边形 $ ABCD $ 中,$ AB = AD $,点 $ B $ 关于 $ AC $ 的对称点 $ B' $ 恰好落在 $ CD $ 上,若 $ \angle BAD = 110^{\circ} $,则 $ \angle ACB $ 的度数为(
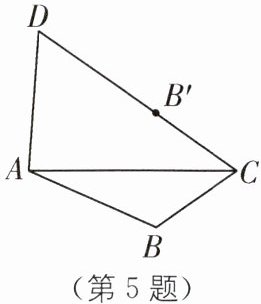
A.$ 40^{\circ} $
B.$ 35^{\circ} $
C.$ 60^{\circ} $
D.$ 70^{\circ} $
B
).
A.$ 40^{\circ} $
B.$ 35^{\circ} $
C.$ 60^{\circ} $
D.$ 70^{\circ} $
答案:
B
6. 如图,在 $ \triangle ABC $ 中,$ AC $ 的垂直平分线交 $ AB $ 于点 $ D $,$ DC $ 平分 $ \angle ACB $,若 $ \angle A = 50^{\circ} $,则 $ \angle B $ 的度数为(
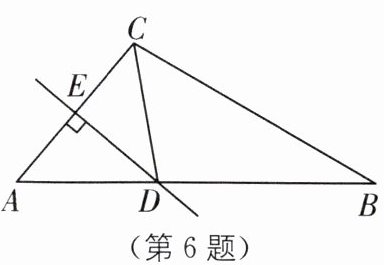
A.$ 25^{\circ} $
B.$ 30^{\circ} $
C.$ 35^{\circ} $
D.$ 40^{\circ} $
B
).
A.$ 25^{\circ} $
B.$ 30^{\circ} $
C.$ 35^{\circ} $
D.$ 40^{\circ} $
答案:
B [解析]本题主要考查了线段垂直平分线的性质以及三角形内角和定理,线段垂直平分线上任意一点,到线段两端点的距离相等.
∵DE垂直平分AC,
∴AD=CD.
∴∠ACD=∠A=50°.又CD平分∠ACB,
∴∠ACB=2∠ACD=100°.
∴∠B=180°−∠A−∠ACB=180°−50°−100°=30°.故选B.
思路引导依据线段垂直平分线的性质,即可得到∠A=∠ACD,再根据角平分线的定义,即可得出∠ACB的度数,根据三角形内角和定理,即可得到∠B的度数.
∵DE垂直平分AC,
∴AD=CD.
∴∠ACD=∠A=50°.又CD平分∠ACB,
∴∠ACB=2∠ACD=100°.
∴∠B=180°−∠A−∠ACB=180°−50°−100°=30°.故选B.
思路引导依据线段垂直平分线的性质,即可得到∠A=∠ACD,再根据角平分线的定义,即可得出∠ACB的度数,根据三角形内角和定理,即可得到∠B的度数.
7. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,作 $ \triangle BCE $,点 $ A $ 在 $ \triangle BCE $ 内,点 $ D $ 在 $ BE $ 上,$ AD $ 垂直平分 $ BE $,且 $ \angle BAC = m^{\circ} $,则 $ \angle BEC $ 的度数为(
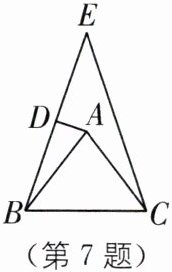
A.$ 90^{\circ} - \frac{1}{2} m^{\circ} $
B.$ 180^{\circ} - 2 m^{\circ} $
C.$ 30^{\circ} + \frac{1}{2} m^{\circ} $
D.$ \frac{1}{2} m^{\circ} $
D
).
A.$ 90^{\circ} - \frac{1}{2} m^{\circ} $
B.$ 180^{\circ} - 2 m^{\circ} $
C.$ 30^{\circ} + \frac{1}{2} m^{\circ} $
D.$ \frac{1}{2} m^{\circ} $
答案:
D
8. 如图,$ \angle 3 = 30^{\circ} $,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证 $ \angle 2 $ 的度数为(
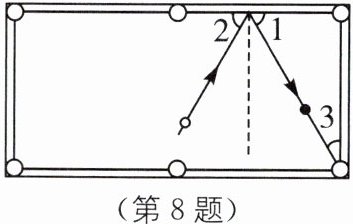
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 75^{\circ} $
C
).
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 75^{\circ} $
答案:
C
9. 把两个全等的等边三角形纸片拼接(不留空隙,不重叠),得到的四边形共有
2
条对称轴.
答案:
2
查看更多完整答案,请扫码查看


