《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

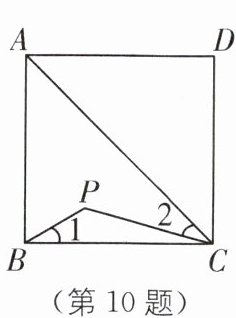
10. 如图,点 $P$ 是正方形 $ABCD$ 内位于对角线 $AC$ 下方的一点,$\angle 1 = \angle 2$,则 $\angle BPC$ 的度数为 $\mathrm{^{\circ}}$。

135

答案： 135　[解析]
∵四边形ABCD是正方形，
∴∠ACB=∠BAC=45°.
∴∠2+∠BCP=45°.
∵∠1=∠2,
∴∠1+∠BCP=45°.
∵∠BPC=180°−∠1−∠BCP,
∴∠BPC=135°.
知识拓展正方形与角有关的性质:
(1)四个角都是直角;
(2)对角线互相垂直;
(3)每条对角线与边的夹角为45°.

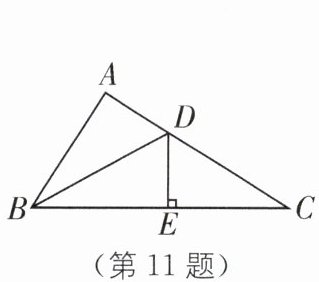
11. 如图,在 $\triangle ABC$ 中,点 $D$、$E$ 分别是边 $AC$、$BC$ 上的点。若 $\triangle ADB \cong \triangle EDB \cong \triangle EDC$,$AB = 10\mathrm{cm}$,则 $BC = $20$\mathrm{cm}$。

答案： 20

12. 如图,$E$、$F$ 是正方形 $ABCD$ 的对角线 $AC$ 上的两点,$AC = 8$,$AE = CF = 2$,则四边形 $BEDF$ 的周长是 8$\sqrt{5}$。

答案： 8$\sqrt{5}$

13. 如图,在四边形 $ABCD$ 中,$\angle ABC = \angle ADC = 90^{\circ}$,$E$ 为对角线 $AC$ 的中点,连接 $BE$、$ED$、$BD$。若 $\angle BAD = 58^{\circ}$,则 $\angle EBD$ 的度数为 $\mathrm{^{\circ}}$。

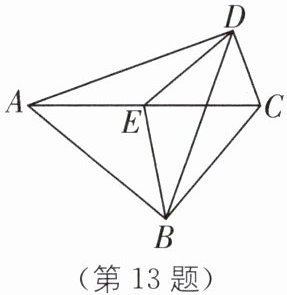
32

答案： 32

14. 如图,将两张长为 $8$、宽为 $2$ 的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值 $8$,那么菱形周长的最大值是17。

答案： 17

15. 已知 $E$ 是正方形 $ABCD$ 的对角线 $AC$ 上一点,$AE = AD$,过点 $E$ 作 $AC$ 的垂线,交边 $CD$ 于点 $F$,那么 $\angle FAD = \mathrm{^{\circ}}$22.5。

答案： 22.5

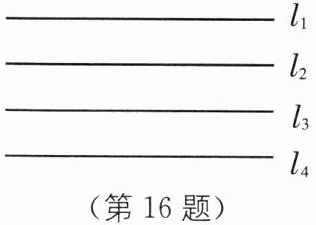
16. 中考新考法 满足条件的结论开放 如图,平面内 $4$ 条直线 $l_1$、$l_2$、$l_3$、$l_4$ 是一组平行线,相邻 $2$ 条平行线间的距离都是 $1$ 个单位长度,正方形 $ABCD$ 的 $4$ 个顶点 $A$、$B$、$C$、$D$ 都在这些平行线上,其中点 $A$、$C$ 分别在直线 $l_1$ 和 $l_4$ 上,该正方形的面积是5或9平方单位。

答案： 5或9

17. 如图,在 $\triangle ABC(AB \neq AC)$ 中,点 $D$、$E$ 在 $BC$ 上,且 $DE = EC$,过点 $D$ 作 $DF // BA$,交 $AE$ 于点 $F$,$AE$ 平分 $\angle BAC$。求证：$DF = AC$。

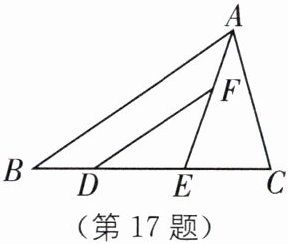
答案：
如图,延长FE到点G,使EG=EF,连接CG.
　　　　　　　　
在△DEF和△CEG中，$\begin{cases}ED = EC，\\∠DEF = ∠CEG，\\FE = EG，\end{cases}$
∴△DEF≌△CEG(SAS).
∴DF=GC,∠DFE=∠G.
∵DF//AB,
∴∠DFE=∠BAE.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴∠G=∠CAE.
∴GC=AC.
∴DF=AC.

18. 如图,在四边形 $ABCD$ 中,对角线 $AC$、$BD$ 相交于点 $O$,且 $AC = BD$。点 $E$、$F$ 分别为 $AB$、$CD$ 的中点,$EF$ 分别交 $BD$、$AC$ 于点 $G$、$H$。求证：$GO = HO$。

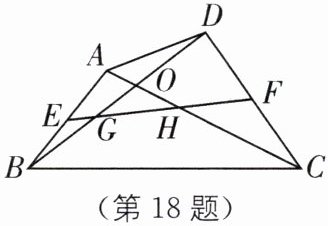
答案： 取BC的中点P,分别连接EP、FP,可证EP=FP,则∠FEP=∠EFP.
又EP//AC,FP//BD,
∴∠FEP=∠OHG,∠EFP=∠OGH.
∴∠OHG=∠OGH.
∴GO=HO.