《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

11. 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草。则他们仅仅少走了8步路。(假设$2步为1m$)

答案： 8 [解析]$\because \angle C = 90^{\circ}$，$AC = 6m$，$BC = 8m$，$\therefore AB^{2}=AC^{2}+BC^{2}=6^{2}+8^{2}=100$，即$AB = 10m$，则$(8 + 6 - 10)×2 = 8$(步)，$\therefore$他们仅仅少走了8步路。

12. 如图,在四边形$ABCD$中,$\angle BAD = \angle BCD = 90^{\circ}$,$AB = AD$,若四边形$ABCD的面积是24cm^{2}$,则$AC$的长是______$cm$。

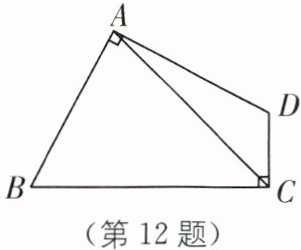
$4\sqrt{3}$

答案： $4\sqrt{3}$

13. 一直角三角形的斜边长比直角边长大$2$,另一直角边长为$6$,则斜边长为10。

答案： 10

14. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,若$c = 3$,则$a^{2} + b^{2} + c^{2} = $18。

答案： 18

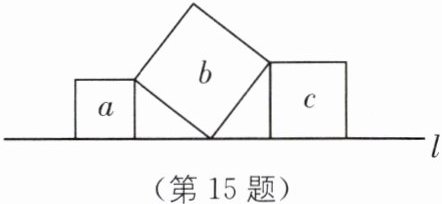
15. 如图,直线$l上有三个正方形a$、$b$、$c$,若$a$、$c的面积分别为5和11$,则$b$的面积为16。

答案： 16

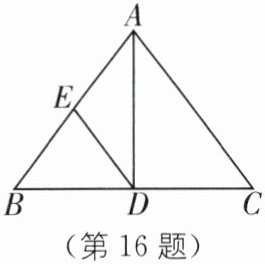
16. 如图,在$\triangle ABC$中,$AB = AC$,$\angle BAC的平分线AD交BC于点D$,$E为AB$的中点,若$BC = 12$,$AD = 8$,则$DE$的长为5。

答案： 5 [解析]本题考查了等腰三角形的性质，勾股定理，直角三角形斜边中线定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型。利用勾股定理求出$AB$，再利用直角三角形斜边中线定理求解即可。$\because AB = AC$，$AD$平分$\angle BAC$，$\therefore AD\perp BC$，$BD = CD = 6$。$\therefore \angle ADB = 90^{\circ}$。$\therefore AB=\sqrt{AD^{2}+BD^{2}}=10$。$\because E$为$AB$的中点，$\therefore DE=\frac{1}{2}AB = 5$。

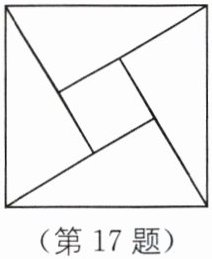
17. 传统文化 赵爽弦图 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示)。如果大正方形的面积是$13$,小正方形的面积是$1$,直角三角形的两直角边分别为$a$、$b$,那么$(a + b)^{2}$的值是______25。

答案： 25

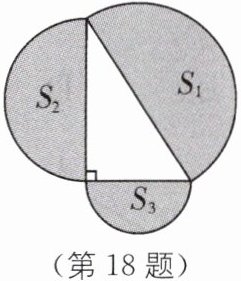
18. 如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积$S_{1} = \frac{25}{8}\pi$,$S_{2} = 2\pi$,则$S_{3} = $$\frac{9}{8}\pi$。

答案： $\frac{9}{8}\pi$

19. 已知三角形的三边长分别是$2n + 1$、$2n^{2} + 2n$、$2n^{2} + 2n + 1$($n$为正整数),则最大角的度数为90$^{\circ}$。

答案： 90

20. 中考新考法 操作探究 动手操作：在矩形纸片$ABCD$中,$AB = 3$,$AD = 5$。如图所示,折叠纸片使点$A落在边BC上的点A'$处,折痕为$PQ$。当点$A'在边BC$上移动时,折痕的端点$P$、$Q$也随之移动。若限定点$P$、$Q分别在边AB$、$AD$上移动,则点$A'在边BC$上可移动的最大距离为______。

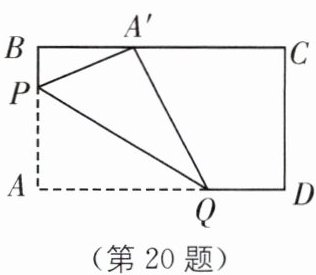
答案：
2 [解析]当点$P$与$B$重合时，$BA'$取最大值是3，当点$Q$与$D$重合时(如图)，由折叠的性质， 得$A'D = AD$，$\because$四边形$ABCD$是矩形，$\therefore AD = BC = 5$，$CD = AB = 3$，$\angle C = 90^{\circ}$，$\therefore A'D = AD = 5$，由勾股定理，得$A'C=\sqrt{A'D^{2}-CD^{2}}=\sqrt{5^{2}-3^{2}}=4$，此时$BA'$取最小值为1，则点$A'$在$BC$边上移动的最大距离：$3 - 1 = 2$。

21. 如图,在四边形$ABCD$中,$AC \perp DC$,$AD = 13cm$,$DC = 12cm$,$AB = 3cm$,$BC = 4cm$,求四边形$ABCD$的面积。

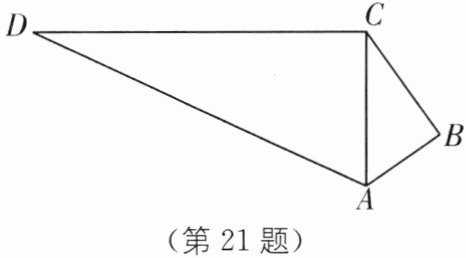
答案： 在$Rt\triangle ACD$中，$AC=\sqrt{AD^{2}-CD^{2}}=\sqrt{13^{2}-12^{2}}=5(cm)$，在$\triangle ABC$中，$\because AB^{2}+BC^{2}=9 + 16 = 25(cm^{2})$，$AC^{2}=5^{2}=25(cm^{2})$，$\therefore AB^{2}+BC^{2}=AC^{2}$。$\therefore \triangle ABC$是直角三角形。$\therefore$四边形$ABCD$的面积$=\frac{1}{2}AB\cdot BC+\frac{1}{2}AC\cdot CD$$=\frac{1}{2}×3×4+\frac{1}{2}×5×12 = 36(cm^{2})$。