《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

11. 某村利用秋冬季节兴修水利,计划请运输公司用 90～150 天(含 90 与 150 天)完成总量为 300 万立方米的土石方运送. 设运输公司完成任务所需的时间为 $ y $(单位：天),平均每天运输土石方量为 $ x $(单位：万立方米),请写出 $ y $ 关于 $ x $ 的函数关系式并给出自变量 $ x $ 的取值范围$ y = \frac{300}{x}(2 \leq x \leq \frac{10}{3}) $.

答案： $ y = \frac{300}{x}(2 \leq x \leq \frac{10}{3}) $

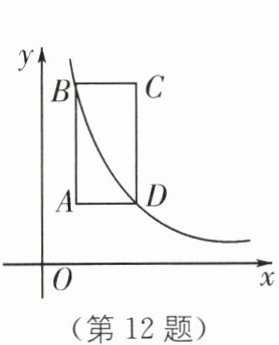
12. 如图,矩形 $ ABCD $ 的边 $ AB $ 与 $ y $ 轴平行,顶点 $ A $ 的坐标为 $ ( 1, 2 ) $,点 $ B $ 与点 $ D $ 在反比例函数 $ y = \frac { 6 } { x } ( x ＞ 0 ) $ 的图像上,则点 $ C $ 的坐标为______(3, 6).

答案： (3, 6)

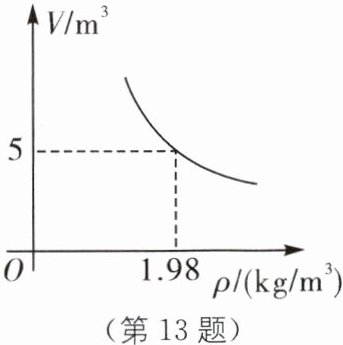
13. 跨学科 密度 一定质量的二氧化碳,其体积 $ V ( \mathrm { m } ^ { 3 } ) $ 是密度 $ \rho ( \mathrm { kg } / \mathrm { m } ^ { 3 } ) $ 的反比例函数,请根据图中的已知条件,写出当 $ \rho = 1.1 \mathrm { kg } / \mathrm { m } ^ { 3 } $ 时二氧化碳的体积 $ V = $9$ \mathrm { m } ^ { 3 } $.

答案： 9

14. 如图,在平面直角坐标系中,过点 $ M ( - 3, 2 ) $ 分别作 $ x $ 轴、$ y $ 轴的垂线与反比例函数 $ y = \frac { 4 } { x } $ 的图像交于 $ A $、$ B $ 两点,则四边形 $ MAOB $ 的面积为10.

答案： 10

15. 如图,已知一次函数 $ y = k x - 4 $ 的图像与 $ x $ 轴、$ y $ 轴分别交于 $ A $、$ B $ 两点,与反比例函数 $ y = \frac { 8 } { x } $ 在第一象限内的图像交于点 $ C $,且 $ A $ 为 $ BC $ 的中点,则 $ k = $4.

答案： 4

16. 在平面直角坐标系 $ x O y $ 中,一次函数 $ y = 10 - x $ 的图像与函数 $ y = \frac { 6 } { x } ( x ＞ 0 ) $ 的图像相交于点 $ A $、$ B $. 设点 $ A $ 的坐标为 $ ( x _ { 1 }, y _ { 1 } ) $,那么长为 $ x _ { 1 } $,宽为 $ y _ { 1 } $ 的矩形的面积为6,周长为20.

答案： 6 20

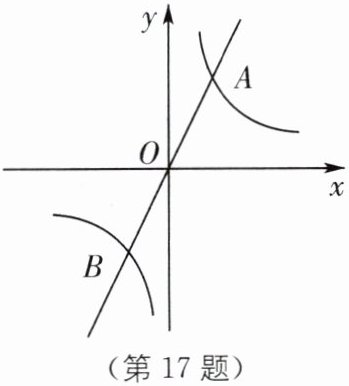
17. 如图,直线 $ y = m x $ 与双曲线 $ y = \frac { k } { x } $ 相交于 $ A $、$ B $ 两点,点 $ A $ 的坐标为 $ ( 1, 2 ) $.
(1) 求反比例函数的表达式；
(2) 根据图像直接写出当 $ m x ＞ \frac { k } { x } $ 时,$ x $ 的取值范围；
(3) 计算线段 $ AB $ 的长.

答案：
(1) 把 $ A(1, 2) $ 代入 $ y = \frac{k}{x} $，得 $ k = 2 $，
即反比例函数的表达式是 $ y = \frac{2}{x} $。
(2) 把 $ A(1, 2) $ 代入 $ y = mx $，得 $ m = 2 $，
即直线的表达式是 $ y = 2x $。
解方程组 $ \begin{cases} y = \frac{2}{x} \\ y = 2x \end{cases} $，得出点 $ B $ 的坐标是 $ (-1, -2) $，
∴当 $ mx ＞ \frac{k}{x} $ 时，$ x $ 的取值范围是 $ -1 ＜ x ＜ 0 $ 或 $ x ＞ 1 $。
(3) 过点 $ A $ 作 $ AC \perp x $ 轴，垂足为 $ C $。
∵ $ A(1, 2) $
∴ $ AC = 2 $，$ OC = 1 $。
∴ $ OA = \sqrt{5} $
∴ $ AB = 2OA = 2\sqrt{5} $。