《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

10. 如图,把矩形 $ ABCD $ 沿直线 $ EF $ 折叠,若 $ \angle 1 = 20^{\circ} $,则 $ \angle 2 = $70°.

答案： 70°

11. 一辆汽车的车牌号在水中的倒影是 $ \text{K} \text{Q} \text{J} 8 \text{d} $,那么它的实际车牌号是K6289.

答案： K6289

12. 如图,$ \triangle ABC $ 与 $ \triangle A'B'C' $ 关于直线 $ l $ 对称,且 $ \angle A = 78^{\circ} $,$ \angle C' = 48^{\circ} $,则 $ \angle B $ 的度数为54°.

答案： 54°

13. 中考新考法 满足条件的结论开放 如图,在 $ \text{Rt} \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ \angle B = 30^{\circ} $,$ ED $ 是 $ BC $ 的垂直平分线,请写出图中两条相等的线段是____.(答案不唯一)

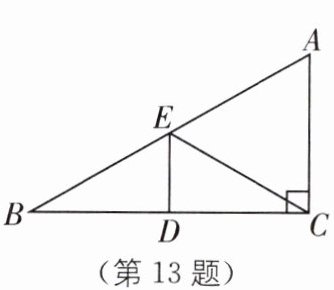
BE=CE

答案： BE=CE=AC=AE或BD=CD

14. 如图,点 $ P $ 是 $ \angle AOC $ 的角平分线上一点,$ PD \perp OA $,垂足为 $ D $,且 $ PD = 3 $,点 $ M $ 是射线 $ OC $ 上一动点,则 $ PM $ 的最小值为3.

答案： 3　[解析]本题考查了垂线段最短、角平分线的性质.根据垂线段最短可知当PM⊥OC时，PM最小，再根据角的平分线的性质，即可得出答案.
　　根据垂线段最短，可知当PM⊥OC时，PM最小，当PM⊥OC时，
　
∵OP平分∠AOC,PD⊥OA,PD=3,
　
∴PM=PD=3.
　　知识拓展
(1)角平分线上的点到角的两边的距离相等;
(2)点到直线的所有连线中，垂线段最短.熟练掌握这些知识是解题的关键.

15. 如图,正方形纸片 $ ABCD $ 的边长为 $ 8 $,将其沿 $ EF $ 折叠,则图中①②③④四个三角形的周长之和为32.

答案： 32

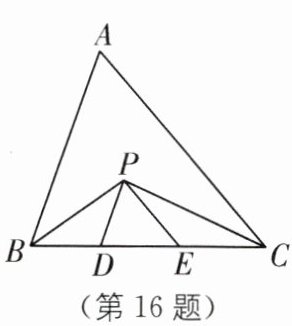
16. 如图,在 $ \triangle ABC $ 中,$ BC = 5 \mathrm{cm} $,$ BP $、$ CP $ 分别是 $ \angle ABC $ 和 $ \angle ACB $ 的角平分线,且 $ PD // AB $,$ PE // AC $,则 $ \triangle PDE $ 的周长是5$ \mathrm{cm} $.

答案： 5

17. 已知 $ \angle AOB $ 和 $ C $、$ D $ 两点,求作点 $ P $,使 $ PC = PD $,且点 $ P $ 到 $ \angle AOB $ 的两边 $ OA $、$ OB $ 的距离相等.

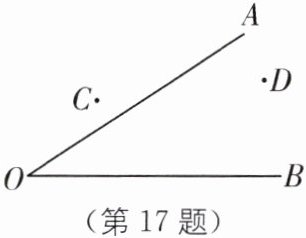
答案：
点P是CD的垂直平分线与∠AOB的角平分线的交点，如图.
　　　　　　　　

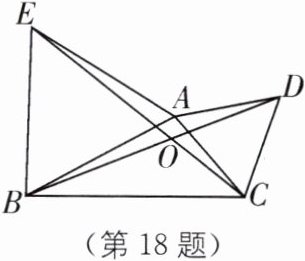
18. 中考新考法 满足结论的条件开放 如图,在 $ \triangle ABC $ 中,分别以 $ AB $、$ AC $ 为边作等边三角形 $ ABE $、$ ACD $,$ BD $ 与 $ CE $ 相交于点 $ O $.
(1)$ EC = BD $ 吗? 为什么?
(2)如果要使 $ \triangle ABE $ 和 $ \triangle ACD $ 全等,那么还需要添加什么条件? 在此条件下,整个图形是轴对称图形吗? 此时 $ \angle BOC $ 是多少度?

答案：
(1)EC=BD.理由如下:
　
∵△ABE、△ACD是等边三角形，
　
∴AE=AB,AD=AC,∠EAB=∠DAC=60°.
∴∠EAB+∠BAC=∠DAC+∠BAC.
　
∴∠EAC=∠DAB.
　
∴△EAC≌△BAD(SAS).
∴EC=BD.
(2)添加条件:AB=AC，整个图形是轴对称图形，此时,∠BOC=120°.