《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

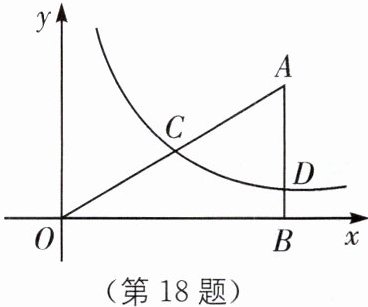
18. 如图,$ \mathrm { Rt } \triangle ABO $ 的顶点 $ O $ 在坐标原点,点 $ B $ 在 $ x $ 轴上,$ \angle ABO = 90 ^ { \circ } $,$ \angle AOB = 30 ^ { \circ } $,$ OB = 2 \sqrt { 3 } $,反比例函数 $ y = \frac { k } { x } ( x ＞ 0 ) $ 的图像经过 $ OA $ 的中点 $ C $,交 $ AB $ 于点 $ D $.
(1) 求反比例函数的关系式；
(2) 连接 $ CD $,求四边形 $ CD B O $ 的面积.

答案：
(1)
∵ $ \angle ABO = 90^{\circ} $，$ \angle AOB = 30^{\circ} $，$ OB = 2\sqrt{3} $，
∴ $ OA = 2AB $，
∴ $ AB = 2 $。
过点 $ C $ 作 $ CE \perp OB $ 于点 $ E $，
∵ $ \angle ABO = 90^{\circ} $，
∴ $ CE // AB $。
∵ $ OC = AC $，
∴ $ OE = BE = \frac{1}{2}OB = \sqrt{3} $，$ CE = \frac{1}{2}AB = 1 $。
∴ $ C(\sqrt{3}, 1) $。
∵反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图像经过 $ OA $ 的中点 $ C $，
∴ $ 1 = \frac{k}{\sqrt{3}} $。
∴ $ k = \sqrt{3} $。
∴反比例函数的关系式为 $ y = \frac{\sqrt{3}}{x} $。
(2)
∵ $ OB = 2\sqrt{3} $，
∴点 $ D $ 的横坐标为 $ 2\sqrt{3} $。
代入 $ y = \frac{\sqrt{3}}{x} $，得 $ y = \frac{1}{2} $，
∴ $ D(2\sqrt{3}, \frac{1}{2}) $。
∴ $ BD = \frac{1}{2} $。
∵ $ AB = 2 $，
∴ $ AD = \frac{3}{2} $。
∴ $ S_{\triangle ACD} = \frac{1}{2}AD \cdot BE = \frac{1}{2} × \frac{3}{2} × \sqrt{3} = \frac{3\sqrt{3}}{4} $。
又 $ S_{\triangle AOB} = \frac{1}{2}OB \cdot AB = \frac{1}{2} × 2\sqrt{3} × 2 = 2\sqrt{3} $，
∴ $ S_{四边形CDBO} = S_{\triangle AOB} - S_{\triangle ACD} = \frac{5\sqrt{3}}{4} $。

19. 某企业生产一种必需商品,经过长期市场调查后发现：商品的月总产量稳定在 600 件. 商品的月销量 $ Q $(件)由基本销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价 $ x $(元/件)$ ( x \leq 10 ) $ 成反比例,且可以得到如下信息：
|售价 $ x $(元/件)|5|8|
|商品的销售量 $ Q $(件)|580|400|
(1) 求 $ Q $ 与 $ x $ 的函数关系式.
(2) 若生产出的商品正好销完,求售价 $ x $.
(3) 求售价 $ x $ 为多少时,月销售额最大,最大值是多少?

答案：
(1) 由题意，设 $ Q = a + \frac{k}{x} $，
由表格可知，当 $ x = 5 $ 时，$ Q = 580 $，当 $ x = 8 $ 时，$ Q = 400 $，
∴ $ \begin{cases} a + \frac{k}{5} = 580 \\ a + \frac{k}{8} = 400 \end{cases} $ 解得 $ \begin{cases} a = 100 \\ k = 2400 \end{cases} $
即 $ Q $ 与 $ x $ 的函数关系式是 $ Q = 100 + \frac{2400}{x}(x \leq 10) $。
(2) 令 $ Q = 600 $，代入函数关系式，得
$ 600 = 100 + \frac{2400}{x} $，解得 $ x = 4.8 $。
故生产的商品正好销完，此时售价 $ x $ 为 4.8。
(3) 设月销售额为 $ w $ 元，
由题意，得 $ w = x(100 + \frac{2400}{x}) = 100x + 2400 $，
∴ $ w $ 随 $ x $ 的增大而增大。
∵ $ x \leq 10 $，
∴当 $ x = 10 $ 时，$ w $ 取得最大值，此时 $ w = 3400 $。
故售价 $ x $ 为 10 时，月销售额最大，最大值是 3400 元。

20. 如图,点 $ A $、$ B $ 分别在 $ x $、$ y $ 轴上,点 $ D $ 在第一象限内,$ DC \perp x $ 轴于点 $ C $,$ AO = CD = 2 $,$ AB = DA = \sqrt { 5 } $,反比例函数 $ y = \frac { k } { x } ( k ＞ 0 ) $ 的图像过 $ CD $ 的中点 $ E $.
(1) 求证：$ \triangle A O B \cong \triangle D C A $；
(2) 求 $ k $ 的值；
(3) $ \triangle B F G $ 和 $ \triangle D C A $ 关于某点成中心对称,其中点 $ F $ 在 $ y $ 轴上,试判断点 $ G $ 是否在反比例函数的图像上,并说明理由.

答案：
(1)
∵点 $ A $、$ B $ 分别在 $ x $、$ y $ 轴上，$ DC \perp x $ 轴，
∴ $ \angle AOB = \angle DCA = 90^{\circ} $。
在 $ Rt\triangle AOB $ 和 $ Rt\triangle DCA $ 中，$ \begin{cases} AO = DC \\ AB = DA \end{cases} $，
∴ $ Rt\triangle AOB \cong Rt\triangle DCA(HL) $。
(2)
∵ $ \angle DCA = 90^{\circ} $，$ DA = \sqrt{5} $，$ CD = 2 $，
∴ $ AC = \sqrt{DA^2 - CD^2} = 1 $。
∴ $ OC = 3 $。
∵ $ E $ 是 $ CD $ 中点，
∴ $ CE = 1 $。
∴ $ E(3, 1) $。
将点 $ E(3, 1) $ 代入 $ y = \frac{k}{x} $，得 $ k = 3 $。
(3) 点 $ G $ 在反比例函数的图像上。理由如下：
∵ $ \triangle BFG $ 和 $ \triangle DCA $ 关于某点成中心对称，
∴ $ \triangle BFG \cong \triangle DCA $。
∴ $ FG = CA = 1 $，$ BF = DC = 2 $，$ \angle BFG = \angle DCA = 90^{\circ} $。而 $ OB = AC = 1 $，
∴ $ OF = OB + BF = 1 + 2 = 3 $。
∴点 $ G $ 的坐标为 $ (1, 3) $。
∵ $ 1 × 3 = 3 $，
∴ $ G(1, 3) $ 在反比例函数 $ y = \frac{3}{x} $ 的图像上。