《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

23. 中考新考法 归纳一般结论 求一个正数的算术平方根,有些数可以直接求得,如$\sqrt {4}$,有些数则不能直接求得,如$\sqrt {5}$,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表：
| n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| $\sqrt{n}$ | 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)表中所给的信息中,你能发现什么规律？(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题：
已知$\sqrt {2.06}\approx 1.435$,求下列各数的算术平方根：①0.0206；②206；③20600.

答案：
(1)被开方数扩大或缩小10²ⁿ倍，这个非负数的算术平方根就相应的扩大或缩小10ⁿ倍；或者说成被开方数的小数点向左或向右移动2n位，算术平方根的小数点就向左或向右移动n位。
(2)①0.1435；②14.35；③143.5。

24. 中考新考法 解题方法型阅读理解题 阅读下面的文字,解答问题.
大家知道$\sqrt {2}$是无理数,而无理数是无限不循环小数,因此$\sqrt {2}$的小数部分我们不可能全部地写出来,于是小明用$\sqrt {2}-1来表示\sqrt {2}$的小数部分,你同意小明的表示方法吗？事实上,小明的表示方法是有道理的,因为$\sqrt {2}$的整数部分是1,用这个数减去其整数部分,差就是小数部分.
请解答：
(1)你能帮我求一下$\sqrt {5}+2$的整数部分和小数部分吗？
(2)已知$10+\sqrt {3}= x+y$,其中x是整数,且$0＜y＜1$,请你帮我确定一下$x-y$的相反数的值.

答案：
(1)
∵4＜5＜9，
∴2＜$\sqrt{5}$＜3。
∴$\sqrt{5}$的整数部分是2，小数部分是$\sqrt{5}$−2。
∴$\sqrt{5}$+2的整数部分是4，小数部分是$\sqrt{5}$−2。
(2)
∵$\sqrt{3}$的整数部分是1，小数部分是$\sqrt{3}$−1，
∴10+$\sqrt{3}$的整数部分是10+1=11，小数部分是$\sqrt{3}$−1。
∴x=11，y=$\sqrt{3}$−1。
∴x−y的相反数为y−x=$\sqrt{3}$−12。

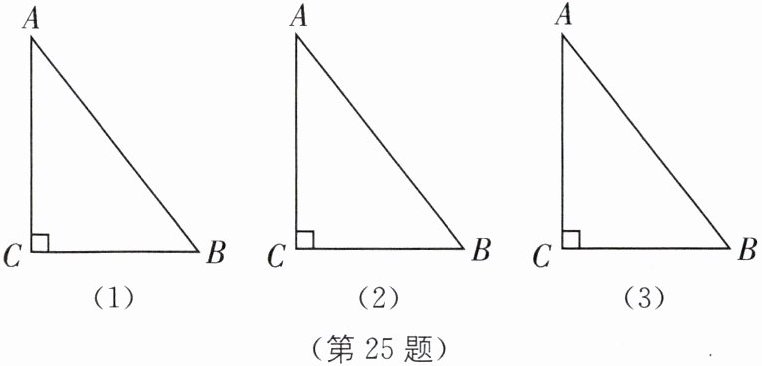
25. 如图(1),有一块直角三角形的绿地,量得两直角边长分别为6m、8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.(图(2)、图(3)备用)

答案：
在Rt△ABC中，∠ACB=90°，AC=8，BC=6。由勾股定理，得AB=10，应分以下三种情况：①如图
(1)，当AB=AD=10时，
∵AC⊥BD，
∴CD=CB=6m。
∴△ABD的周长为10+10+2×6=32m。 ②如图
(2)，当AB=BD=10时，
∵BC=6m，
∴CD=10−6=4m。
∴AD=$\sqrt{AC²+CD²}$=$\sqrt{8²+4²}$=4$\sqrt{5}$m。
∴△ABD的周长为10+10+4$\sqrt{5}$=(20+4$\sqrt{5}$)m。③如图
(3)，当AB为底时，设AD=BD=x，则CD=x−6。由勾股定理，得AD=$\sqrt{AC²+CD²}$=$\sqrt{8²+(x−6)²}$=x，则x=$\frac{25}{3}$。
∴△ABD的周长为$\frac{25}{3}$+$\frac{25}{3}$+10=$\frac{80}{3}$m。