《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

1. 计算$-(\sqrt {2})^{2}+(\sqrt {2}+π)^{0}+(-\frac {1}{2})^{-2}$的结果是(D).
A.1
B.2
C.$\frac {11}{4}$
D.3

答案： D

2. 四个实数1、0、$\sqrt {3}$、-3中,最大的是(C).
A.1
B.0
C.$\sqrt {3}$
D.-3

答案： C　[解析]此题主要考查了实数运算，正确掌握实数比较大小的方法是解题关键。四个实数1,0,$\sqrt{3}$,−3中，−3＜0＜1＜$\sqrt{3}$，故最大的数是$\sqrt{3}$。故选C。知识拓展：实数的大小比较：正数＞0＞负数，绝对值大的负数反而小，绝对值小的负数反而大。

3. 若$\sqrt {3}＜a＜\sqrt {10}$,则下列结论中正确的是(B).
A.$1＜a＜3$
B.$1＜a＜4$
C.$2＜a＜3$
D.$2＜a＜4$

答案： B

4. 若$\sqrt {x-1}-\sqrt {1-x}= (x+y)^{2}$,则$x-y$的值为(C).
A.-1
B.1
C.2
D.3

答案： C

5. 下列各式化简结果为无理数的是(C).
A.$\sqrt [3]{-27}$
B.$(\sqrt {2}-1)^{0}$
C.$\sqrt {8}$
D.$\sqrt {(-2)^{2}}$

答案： C

6. 设n为正整数,且$n＜\sqrt {65}＜n+1$,则n的值为(D).
A.5
B.6
C.7
D.8

答案： D

7. 如图,数轴上A、B两点表示的数分别为$\sqrt {2}$和5.1,则A、B两点之间表示整数的点共有(C).

A.6个
B.5个
C.4个
D.3个

答案： C

8. 已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是(C).
①m是无理数；
②m是方程$m^{2}-12= 0$的解；
③m满足不等式组$\left\{\begin{array}{l} m-4＞0,\\ m-5＜0;\end{array} \right. $
④m是12的算术平方根.
A.①②
B.①③
C.③
D.①②④

答案： C

9. 计算：$\sqrt [3]{-8}=$−2.

答案： −2

10. $1-\sqrt {3}$的相反数是$\sqrt{3}-1$；$\sqrt [3]{-27}$的绝对值是3.

答案： $\sqrt{3}$−1；3

11. 若$\sqrt {a}= 4$,则$a= $16.

答案： 16

12. 已知m、n为两个连续的整数,且$m＜\sqrt {11}＜n$,则$m+n= $7.

答案： 7

13. 若将三个数$-\sqrt {3}$、$\sqrt {7}$、$\sqrt {11}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{7}$.

答案： $\sqrt{7}$

14. 实数a、b在数轴上的位置如图所示,则$\sqrt {a^{2}}-|a-b|=$−b.

答案： −b

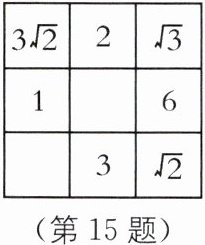
15. 在如图方格中,若要使横、竖、斜对角的3个实数相乘都得到同样的结果,则2个空格的实数之积为____.

6$\sqrt{2}$

答案： 6$\sqrt{2}$　[解析]本题考查了二次根式的乘法运算法则，熟练掌握二次根式的加减乘除运算法则是解决此类题的关键。先将表格中最上一行的3个数相乘得到6$\sqrt{6}$，然后中间一行的三个数相乘以及最后一行的三个数相乘都是6$\sqrt{6}$，即可求解。由题意可知，第一行三个数的乘积为3$\sqrt{2}$×2×$\sqrt{3}$=6$\sqrt{6}$，设第二行中间数为x，则1×x×6=6$\sqrt{6}$，解得x=$\sqrt{6}$，设第三行第一个数为y，则y×3×$\sqrt{2}$=6$\sqrt{6}$，解得y=2$\sqrt{3}$。
∴2个空格的实数之积为xy=2$\sqrt{18}$=6$\sqrt{2}$。知识拓展：二次根式的乘除混合运算，从左到右依次计算。二次根式相乘，把系数相乘作为积的系数，被开方数相乘，并化为最简二次根式；二次根式相除，把系数相除作为商的系数，被开方数相除，并化为最简二次根式。

16. 已知一个正数的两个不同的平方根是$3x-2$和$4-x$,则$x=$−1.

答案： −1

17. 规定用符号$[x]$表示一个实数的整数部分,例如$[3.69]= 3$,$[\sqrt {3}]= 1$,按此规定,$[\sqrt {13}-1]=$2.

答案： 2