第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
19. 如图,在 $\triangle ABC$ 中,$D$、$E$ 分别是 $AB$、$AC$ 的中点,$BE = 2DE$,延长 $DE$ 到点 $F$,使得 $EF = BE$,连接 $CF$。
(1)求证:四边形 $BCFE$ 是菱形;
(2)若 $CE = 4$,$\angle BCF = 120^{\circ}$,求菱形 $BCFE$ 的面积。
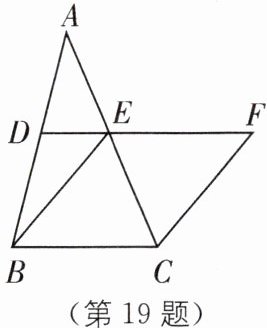
(1)求证:四边形 $BCFE$ 是菱形;
(2)若 $CE = 4$,$\angle BCF = 120^{\circ}$,求菱形 $BCFE$ 的面积。

答案:
(1)
∵D、E分别是AB、AC的中点,
∴DE//BC且2DE=BC.
又BE=2DE,EF=BE,
∴EF=BC.
又EF//BC,
∴四边形BCFE是平行四边形.
∵BE=FE,
∴四边形BCFE是菱形.
(2)
∵∠BCF=120°,
∴∠EBC=60°.
∴△EBC是等边三角形.
∴菱形的边长为4,高为2$\sqrt{3}$
∴菱形的面积为4×2$\sqrt{3}$=8$\sqrt{3}$
(1)
∵D、E分别是AB、AC的中点,
∴DE//BC且2DE=BC.
又BE=2DE,EF=BE,
∴EF=BC.
又EF//BC,
∴四边形BCFE是平行四边形.
∵BE=FE,
∴四边形BCFE是菱形.
(2)
∵∠BCF=120°,
∴∠EBC=60°.
∴△EBC是等边三角形.
∴菱形的边长为4,高为2$\sqrt{3}$
∴菱形的面积为4×2$\sqrt{3}$=8$\sqrt{3}$
20. 如图,在菱形 $ABCD$ 中,$F$ 为边 $BC$ 的中点,$DF$ 与对角线 $AC$ 交于点 $M$,过 $M$ 作 $ME \perp CD$ 于点 $E$,$\angle 1 = \angle 2$。
(1)若 $CE = 1$,求 $BC$ 的长;
(2)求证:$AM = DF + ME$。

(1)若 $CE = 1$,求 $BC$ 的长;
(2)求证:$AM = DF + ME$。

答案:
(1)BC=2.
(2)延长DF、AB交于点N.
∵四边形ABCD是菱形,
∴∠FCM=∠ECM.
又F为边BC的中点,
∴CF=BF=$\frac{1}{2}$BC=$\frac{1}{2}$CD.
易证CE=ED=$\frac{1}{2}$CD,
∴△CMF≌△CME.
∴MF=ME.
∵AB//CD,
∴∠2=∠N,∠NBF=∠DCF.
又BF=CF,
∴△CDF≌BNF.
∴NF=DF.又∠1=∠2,
∴∠N=∠1.
∴AM=MN=NF+MF=DF+ME.
(1)BC=2.
(2)延长DF、AB交于点N.
∵四边形ABCD是菱形,
∴∠FCM=∠ECM.
又F为边BC的中点,
∴CF=BF=$\frac{1}{2}$BC=$\frac{1}{2}$CD.
易证CE=ED=$\frac{1}{2}$CD,
∴△CMF≌△CME.
∴MF=ME.
∵AB//CD,
∴∠2=∠N,∠NBF=∠DCF.
又BF=CF,
∴△CDF≌BNF.
∴NF=DF.又∠1=∠2,
∴∠N=∠1.
∴AM=MN=NF+MF=DF+ME.
21. 如图,四边形 $ABCD$ 是正方形,$M$ 是边 $BC$ 上的一点,$E$ 是边 $CD$ 的中点,$AE$ 平分 $\angle DAM$。
(1)求证:$AM = AD + MC$。
(2)$AM = DE + BM$ 是否成立?若成立,请给出证明;若不成立,请说明理由。
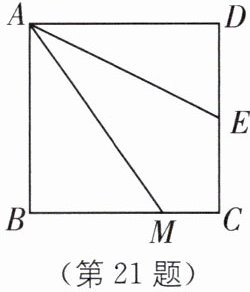
(1)求证:$AM = AD + MC$。
(2)$AM = DE + BM$ 是否成立?若成立,请给出证明;若不成立,请说明理由。

答案:
(1)延长AE、BC交于点N,如图
(1).
∵四边形ABCD是正方形,
∴AD//BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴MA=MN.
在△ADE和△NCE中,$\begin{cases}∠DAE = ∠CNE,\\∠AED = ∠NEC,\\DE = CE,\end{cases}$
∴△ADE≌△NCE(AAS).
∴AD=NC.
∴MA=MN=NC+MC=AD+MC.

(2)AM=DE+BM成立.证明如下:
过点A作AF⊥AE,交CB的延长线于点F,如图
(2)所示.
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB//DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°−∠BAE=∠DAE.
在△ABF和△ADE中,$\begin{cases}∠FAB = ∠EAD,\\AB = AD,\\∠ABF = ∠D,\end{cases}$
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB//DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM +∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
(1)延长AE、BC交于点N,如图
(1).
∵四边形ABCD是正方形,
∴AD//BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴MA=MN.
在△ADE和△NCE中,$\begin{cases}∠DAE = ∠CNE,\\∠AED = ∠NEC,\\DE = CE,\end{cases}$
∴△ADE≌△NCE(AAS).
∴AD=NC.
∴MA=MN=NC+MC=AD+MC.

(2)AM=DE+BM成立.证明如下:
过点A作AF⊥AE,交CB的延长线于点F,如图
(2)所示.
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB//DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°−∠BAE=∠DAE.
在△ABF和△ADE中,$\begin{cases}∠FAB = ∠EAD,\\AB = AD,\\∠ABF = ∠D,\end{cases}$
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB//DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM +∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
查看更多完整答案,请扫码查看


