《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

20. $A$、$B$两地相距15km,甲、乙两人同时从$A出发去B$。甲先乘汽车到达$A$、$B之间的C$地,然后下车步行,乙全程骑自行车,结果两人同时到达。已知甲步行的速度是乙骑自行车速度的一半,乙骑自行车的速度是甲乘汽车速度的一半,求$C地与A$地间的距离。

答案： C 地与 A 地间的距离为 10 km。

21. (全国初中数学联赛)已知四边形$ABCD$的面积为32,$AB$、$CD$、$AC$的长都是整数,且它们的和为16。
(1)这样的四边形有几个？
(2)求这样的四边形边长的平方和的最小值。

答案：
(1) 记 $ AB = a $，$ CD = b $，$ AC = l $，并设 $ \triangle ABC $ 的边 AB 上的高为 $ h_1 $，$ \triangle ADC $ 的边 DC 上的高为 $ h_2 $。则 $ S_{四边形ABCD} = S_{\triangle ABC} + S_{\triangle ADC} = \frac{1}{2}(h_1a + h_2b) \leq \frac{1}{2}l(a + b) $，仅当 $ h_1 = h_2 = l $ 时等号成立。即在四边形 ABCD 中，当 $ AC \perp AB $，$ AC \perp CD $ 时，等号成立。由已知，得 $ 64 \leq l(a + b) $。又由题设 $ a + b = 16 - l $，可得 $ 64 \leq l(16 - l) = 64 - (l - 8)^2 \leq 64 $。于是 $ l = 8 $，$ a + b = 8 $，且这时 $ AC \perp AB $，$ AC \perp CD $。因此，这样的四边形有如下 4 个：$ a = 1 $，$ b = 7 $，$ l = 8 $；$ a = 2 $，$ b = 6 $，$ l = 8 $；$ a = 3 $，$ b = 5 $，$ l = 8 $；$ a = b = 4 $，$ l = 8 $。
(2) 又由 $ AB = a $，$ CD = 8 - a $，则 $ BC^2 = 8^2 + a^2 $，$ AD^2 = 8^2 + (8 - a)^2 $。因此，这样的四边形的边长的平方和为 $ 2a^2 + 2(8 - a)^2 + 128 = 4(a - 4)^2 + 192 $。故当 $ a = b = 4 $ 时，平方和最小，且为 192。

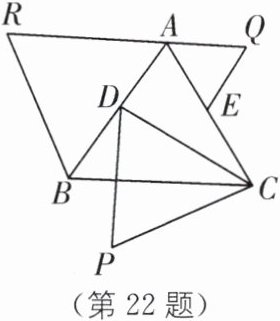
22. (江苏省第十六届初中数学竞赛)如图,已知等边三角形$ABC$,在$AB上取点D$,在$AC上取点E$,使得$AD = AE$,作等边三角形$PCD$、$QAE和RAB$,求证：$P$、$Q$、$R$是等边三角形的三个顶点。

答案： 连接 BP。$ \because \triangle ABC $ 和 $ \triangle PCD $ 都为等边三角形，$ \therefore AC = BC $，$ DC = PC $，$ \angle ACB = \angle DCP = 60^\circ $。$ \therefore \angle ACB - \angle DCB = \angle DCP - \angle DCB $，即 $ \angle ACD = \angle BCP $。$ \therefore \triangle ACD \cong \triangle BCP (SAS) $。$ \therefore AD = BP $。又 $ \angle RAB + \angle BAC + \angle QAE = 180^\circ $，$ \therefore R $、$ A $、$ Q $ 三点共线。又 $ \angle CBP = \angle CAD = 60^\circ $，$ \angle RBA + \angle ABC + \angle CBP = 180^\circ $，$ \therefore R $、$ B $、$ P $ 三点共线。又 $ AQ = AE = AD = BP $，$ \therefore RQ = RA + AQ = RB + BP = RP $。又 $ \angle R = 60^\circ $，$ \therefore \triangle PQR $ 是等边三角形。则 $ P $、$ Q $、$ R $ 是等边三角形的三个顶点。