《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

11. 若□ABCD的周长为60cm,对角线相交于点O,△AOB的周长比△BOC的周长多8cm,则AB=19cm,BC=11cm。

答案： 19 11

12. 在□ABCD中,一角的平分线把一条边分成3cm和4cm两部分,则□ABCD的周长为20 cm或22 cm。

答案： 20 cm或22 cm

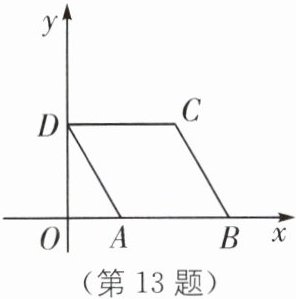
13. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形ABCD中,AB= 2,∠DAB= 120°.如图,建立平面直角坐标系xOy,使得边AB在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是(2,√3)。

答案： (2,√3)

14. 如图,在矩形ABCD中,AB= 2,BC= 5,MN//AB交AD于点M,交BC于点N,在MN上任取两点P、Q,那么图中阴影部分的面积是5。

答案： 5

15. 如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是5。

答案： 5

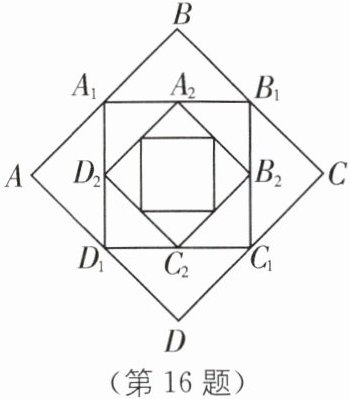
16. 如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形$A_1B_1C_1D_1,$顺次连接正方形$A_1B_1C_1D_1$四边的中点得到第二个正方形$A_2B_2C_2D_2……$以此类推,则第六个正方形$A_6B_6C_6D_6$的周长是1/2。

答案： 1/2

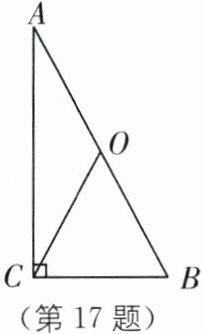
17. 如图,利用矩形的性质,证明“直角三角形斜边上的中线等于斜边的一半”。
已知：______；
求证：______；
证明：

答案：
已知：在Rt△ABC中，∠ACB=90°，CO是斜边AB边上的中线.
求证：CO=1/2AB.
证明：如图，延长CO至点E，使CO=OE，连接AE、BE，
∵CO=OE，点O为AB中点，
∴OA=OB，
∴四边形ACBE为平行四边形.
∵∠ACB=90°，
∴平行四边形AEBC是矩形，
∴CE=AB.
∵CO=1/2CE，
∴CO=1/2AB.

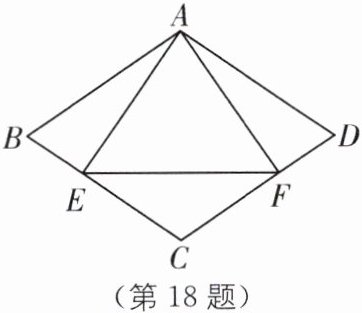
18. 如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,连接EF.
(1)求证：AE= AF；
(2)若∠B= 60°,求∠AEF的度数。

答案：
(1)
∵四边形ABCD是菱形，
∴AB=AD，∠B=∠D.
又AE⊥BC于点E，AF⊥CD于点F，
∴∠AEB=∠AFD=90°.
在△ABE与△ADF中，{∠B=∠D，∠AEB=∠AFD，AB=AD，
∴△ABE≌△ADF(AAS).
∴AE=AF.
(2)
∵四边形ABCD是菱形，
∴∠B+∠BAD=180°.
∵∠B=60°，
∴∠BAD=120°.
又∠AEB=90°，∠B=60°，
∴∠BAE=30°.
由
(1)知△ABE≌△ADF，
∴∠BAE=∠DAF=30°.
∴∠EAF=120°-30°-30°=60°. 又AE=AF，
∴△AEF是等边三角形.
∴∠AEF=60°.