第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD \perp AB$,垂足为$D$,点$E是AB$的中点,$CD = DE = a$,则$AB$的长为(

A.$2a$
B.$2\sqrt{2}a$
C.$3a$
D.$\frac{4\sqrt{3}}{3}a$
B
)。
A.$2a$
B.$2\sqrt{2}a$
C.$3a$
D.$\frac{4\sqrt{3}}{3}a$
答案:
B
2. 分别以下列四组数为一个三角形的三边的长:①$6$、$8$、$10$;②$5$、$12$、$13$;③$8$、$15$、$17$;④$7$、$8$、$9$。其中能构成直角三角形的有(
A.$4$组
B.$3$组
C.$2$组
D.$1$组
B
)。A.$4$组
B.$3$组
C.$2$组
D.$1$组
答案:
B
3. 将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形(
A.可能是锐角三角形
B.不可能是直角三角形
C.仍然是直角三角形
D.可能是钝角三角形
C
)。A.可能是锐角三角形
B.不可能是直角三角形
C.仍然是直角三角形
D.可能是钝角三角形
答案:
C
4. 一个直角三角形,两直角边长分别为$3和4$,下列说法正确的是(
A.斜边长为$5$
B.三角形的周长为$25$
C.斜边长为$25$
D.三角形的面积为$20$
A
)。A.斜边长为$5$
B.三角形的周长为$25$
C.斜边长为$25$
D.三角形的面积为$20$
答案:
A
5. 如图,在$Rt\triangle ABC$中,$CM平分\angle ACB交AB于点M$,过点$M作MN // BC交AC于点N$,且$MN平分\angle AMC$,若$AN = 1$,则$BC$的长为(

A.$4$
B.$6$
C.$4\sqrt{3}$
D.$8$
B
)。
A.$4$
B.$6$
C.$4\sqrt{3}$
D.$8$
答案:
B
6. 在$\triangle ABC$中,$\angle A$、$\angle B$、$\angle C的对边分别是a$、$b$、$c$,下列说法不正确的是(
A.若$\angle C - \angle B = \angle A$,则$\triangle ABC$是直角三角形
B.若$c^{2} = b^{2} - a^{2}$,则$\triangle ABC$是直角三角形,且$\angle C = 90^{\circ}$
C.若$(c + a)(c - a) = b^{2}$,则$\triangle ABC$是直角三角形
D.若$\angle A:\angle B:\angle C = 5:2:3$,则$\triangle ABC$是直角三角形
B
)。A.若$\angle C - \angle B = \angle A$,则$\triangle ABC$是直角三角形
B.若$c^{2} = b^{2} - a^{2}$,则$\triangle ABC$是直角三角形,且$\angle C = 90^{\circ}$
C.若$(c + a)(c - a) = b^{2}$,则$\triangle ABC$是直角三角形
D.若$\angle A:\angle B:\angle C = 5:2:3$,则$\triangle ABC$是直角三角形
答案:
B
7. 如图,在$\triangle ABC$中,$AD \perp BC$,$CE \perp AB$,垂足分别为$D$、$E$,$AD$、$CE交于点H$,已知$EH = EB = 3$,$AE = 4$,则$CH$的长是(

A.$1$
B.$2$
C.$3$
D.$4$
A
)。
A.$1$
B.$2$
C.$3$
D.$4$
答案:
A
8. 如图,矩形$ABCD边AD沿折痕AE$折叠,使点$D落在BC上的点F$处,已知$AB = 6$,$\triangle ABF的面积是24$,则$FC$等于(
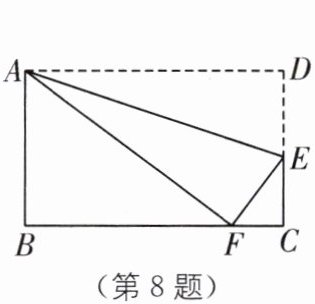
A.$1$
B.$2$
C.$3$
D.$4$
B
)。
A.$1$
B.$2$
C.$3$
D.$4$
答案:
B
9. 如图,在高为$5m$,坡面长为$13m$的楼梯表面铺地毯,地毯的长度至少需要(
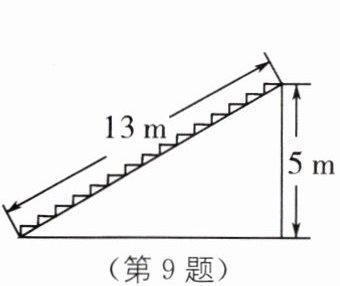
A.$17m$
B.$18m$
C.$25m$
D.$26m$
A
)。
A.$17m$
B.$18m$
C.$25m$
D.$26m$
答案:
A
10. 中考新考法 归纳一般结论 如图,$\triangle OA_{1}A_{2}$为等腰直角三角形,$OA_{1} = 1$,以斜边$OA_{2}为直角边作等腰直角三角形OA_{2}A_{3}$,再以$OA_{3}为直角边作等腰直角三角形OA_{3}A_{4}$,…$$,按此规律作下去,则$OA_{n}$的长度为(
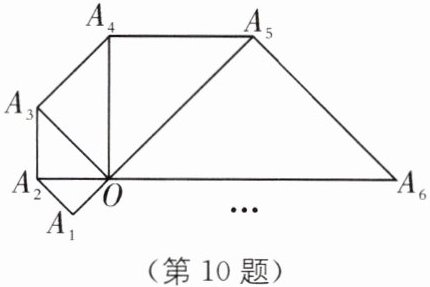
A.$(\sqrt{2})^{n}$
B.$(\sqrt{2})^{n - 1}$
C.$(\frac{\sqrt{2}}{2})^{n}$
D.$(\frac{\sqrt{2}}{2})^{n - 1}$
B
)。
A.$(\sqrt{2})^{n}$
B.$(\sqrt{2})^{n - 1}$
C.$(\frac{\sqrt{2}}{2})^{n}$
D.$(\frac{\sqrt{2}}{2})^{n - 1}$
答案:
B [解析]本题考查等腰直角三角形的性质以及勾股定理,解答本题先要计算出$OA_{1}$、$OA_{2}$、$OA_{3}$的值,然后再找出规律。$\because \triangle OA_{1}A_{2}$为等腰直角三角形,$OA_{1}=1$,$\therefore OA_{2}=\sqrt{2}$;$\because \triangle OA_{2}A_{3}$为等腰直角三角形,$\therefore OA_{3}=2=(\sqrt{2})^{2}$;$\because \triangle OA_{3}A_{4}$为等腰直角三角形,$\therefore OA_{4}=2\sqrt{2}=(\sqrt{2})^{3}$;$\because \triangle OA_{4}A_{5}$为等腰直角三角形,$\therefore OA_{5}=4=(\sqrt{2})^{4}$;…$\therefore OA_{n}$的长度为$(\sqrt{2})^{n - 1}$。故选B。方法诠释:这种规律的探究,一般需要先求出前几个图形中的线段的长度,并把它写成一列,可列表表示出来,然后把数值与序号进行关联,本题中$\sqrt{2}$的指数与序号相差1,所以$OA_{n}$的长度为$(\sqrt{2})^{n - 1}$。
查看更多完整答案,请扫码查看


