《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

12. (“祖冲之杯”数学竞赛)已知四条直线：$y = kx - 3$,$y = -1$,$y = 3$,$x = 1$所围成的四边形面积是12,则$k$的值是-2 或 1。

答案： -2 或 1

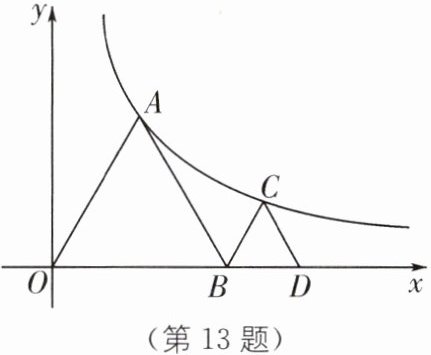
13. (全国初中数学竞赛)如图,点$A$、$C都在函数y = \frac{3\sqrt{3}}{x}(x＞0)$的图像上,点$B$、$D都在x$轴上,且使得$\triangle OAB$、$\triangle BCD$都是等边三角形,则点$D$的坐标为____$ (2\sqrt{6}, 0) $。

答案： $ (2\sqrt{6}, 0) $

14. 已知$xy = 3$,那么$x\sqrt{\frac{y}{x}} + y\sqrt{\frac{x}{y}}$的值为$\pm 2\sqrt{3}$。

答案： $ \pm 2\sqrt{3} $

15. (第二十届“希望杯”全国数学邀请赛)对于正整数$k$,记直线$y = -\frac{k}{k + 1}x + \frac{1}{k + 1}$与坐标轴所围成的直角三角形的面积为$S_k$,则$S_k = $$\frac{1}{2k(k + 1)}$,$S_1 + S_2 + S_3 + S_4 = $$\frac{2}{5}$。

答案： $ \frac{1}{2k(k + 1)} $ $ \frac{2}{5} $

16. 已知$\sqrt{a - 1} + (ab - 2)^2 = 0$,则$\frac{1}{ab} + \frac{1}{(a + 1)(b + 1)} + … + \frac{1}{(a + 2023)(b + 2023)}$的值为$\frac{2024}{2025}$。

答案： $ \frac{2024}{2025} $

17. 用你发现的规律解答下列问题：
$\frac{1}{1×2} = 1 - \frac{1}{2}$；$\frac{1}{2×3} = \frac{1}{2} - \frac{1}{3}$；$\frac{1}{3×4} = \frac{1}{3} - \frac{1}{4}$；…$$。
(1)计算：$\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \frac{1}{4×5} + \frac{1}{5×6} = $$\frac{5}{6}$；
(2)探究：$\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + … + \frac{1}{n(n + 1)} = $$\frac{n}{n + 1}$；(用含有$n$的式子表示)
(3)若$\frac{1}{1×3} + \frac{1}{3×5} + \frac{1}{5×7} + … + \frac{1}{(2n - 1)(2n + 1)}$的值为$\frac{17}{35}$,求$n$的值。
$n = 17$

答案：
(1) $ \frac{5}{6} $
(2) $ \frac{n}{n + 1} $
(3) $ n = 17 $

18. 当$k$为何值时,多项式$x^2 - 2xy + ky^2 + 3x - 5y + 2$能分解成两个一次因式的积？

答案： 设 $ x^2 - 2xy + ky^2 + 3x - 5y + 2 = (x + ay + 2)(x + by + 1) $，则 $ a + b = -2 $，$ ab = k $，$ a + 2b = -5 $。解得 $ k = -3 $。

19. 甲、乙两人两次同时在同一粮店购买粮食(假设两次购买的单价不同),甲每次购买粮食100kg,乙每次购买粮食用去100元。设甲、乙两人第一次购买粮食的单价为$x$元/kg,第二次单价为$y$元/kg。
(1)用含$x$、$y$的代数式表示甲两次购买粮食共需付款$(100x + 100y)$元,乙两次共购买$\left( \frac{100}{x} + \frac{100}{y} \right)$kg粮食。若甲两次购买粮食的平均单价为每千克$Q_1$元,乙两次购粮的平均单价为每千克$Q_2$元,则$Q_1 = $$\frac{x + y}{2}$,$Q_2 = $$\frac{2xy}{x + y}$；
(2)若规定谁两次购粮的平均单价低,谁的购粮方式就更合算,请你判断甲、乙两人的购粮方式哪一个更合算些,并说明理由。
要判定谁的购粮方式合算，就是判定 $ Q_1 $ 与 $ Q_2 $ 的大小，小的合算。$ \because Q_1 - Q_2 = \frac{x + y}{2} - \frac{2xy}{x + y} = \frac{(x - y)^2}{2(x + y)} $，又 $ x \neq y $，$ \therefore (x - y)^2 ＞ 0 $。而 $ 2(x + y) ＞ 0 $，$ \therefore Q_1 - Q_2 ＞ 0 $，即 $ Q_1 ＞ Q_2 $。即乙的购粮方式更合算。

答案：
(1) $ (100x + 100y) $ $ \left( \frac{100}{x} + \frac{100}{y} \right) $ $ \frac{x + y}{2} $ $ \frac{2xy}{x + y} $
(2) 要判定谁的购粮方式合算，就是判定 $ Q_1 $ 与 $ Q_2 $ 的大小，小的合算。$ \because Q_1 - Q_2 = \frac{x + y}{2} - \frac{2xy}{x + y} = \frac{(x - y)^2}{2(x + y)} $，又 $ x \neq y $，$ \therefore (x - y)^2 ＞ 0 $。而 $ 2(x + y) ＞ 0 $，$ \therefore Q_1 - Q_2 ＞ 0 $，即 $ Q_1 ＞ Q_2 $。即乙的购粮方式更合算。