《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

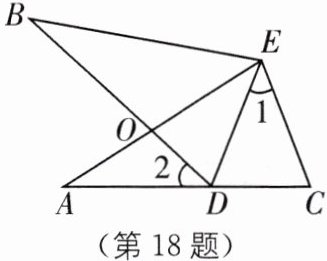
18. 如图,$\angle A = \angle B$,$AE = BE$,点$D在AC$边上,$\angle 1 = \angle 2$,$AE和BD相交于点O$。
(1)求证：$\triangle AEC\cong\triangle BED$；
(2)若$\angle 1 = 42^{\circ}$,求$\angle BDE$的度数。

答案：
(1)$\because AE$和$BD$相交于点$O$，
$\therefore \angle AOD=\angle BOE$。
在$\triangle AOD$和$\triangle BOE$中，$\angle A=\angle B$，
$\therefore \angle BEO=\angle 2$。
又$\angle 1=\angle 2,\therefore \angle 1=\angle BEO$。
$\therefore \angle 1+\angle OED=\angle BEO+\angle OED$，
即$\angle AEC=\angle BED$。
在$\triangle AEC$和$\triangle BED$中，
$\begin{cases}\angle A=\angle B,\\AE = BE,\\\angle AEC=\angle BED,\end{cases}$
$\therefore \triangle AEC\cong \triangle BED(ASA)$。
(2)$\because \triangle AEC\cong \triangle BED$，
$\therefore EC = ED,\angle C=\angle BDE$。
在$\triangle EDC$中，$\because EC = ED,\angle 1 = 42^{\circ}$，
$\therefore \angle C=\angle EDC = 69^{\circ}$。
$\therefore \angle BDE=\angle C = 69^{\circ}$。

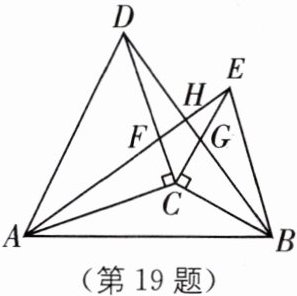
19. 如图,$\triangle ACD和\triangle BCE$都是等腰直角三角形,$\angle ACD = \angle BCE = 90^{\circ}$,$AE交DC于点F$,$BD分别交CE$、$AE于点G$、$H$。试猜测线段$AE和BD$的数量和位置关系,并说明理由。

答案： 猜测$AE = BD,AE\perp BD$。理由如下：
$\because \triangle ACD$和$\triangle BCE$都是等腰直角三角形，
$\therefore AC = DC,EC = BC,\angle ACD=\angle BCE = 90^{\circ}$。
$\therefore \angle ACD+\angle DCE=\angle BCE+\angle DCE$，
即$\angle ACE=\angle DCB$。
在$\triangle ACE$与$\triangle DCB$中，$\begin{cases}AC = DC,\\\angle ACE=\angle DCB,\\EC = BC,\end{cases}$
$\therefore \triangle ACE\cong \triangle DCB(SAS)$。
$\therefore AE = BD,\angle CAE=\angle CDB$。
$\because \angle CAF+\angle AFC = 90^{\circ},\angle AFC=\angle DFH$，
$\angle CAF=\angle FDH$，
$\therefore \angle FDH+\angle DFH = 90^{\circ}$。
$\therefore \angle FHD = 90^{\circ}.\therefore AE\perp BD$。

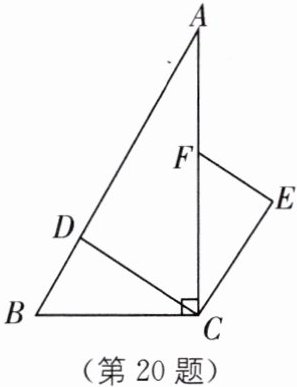
20. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,点$D$、$F分别在AB$、$AC$上,$CF = CB$,连接$CD$,将线段$CD绕点C按顺时针方向旋转90^{\circ}后得CE$,连接$EF$。
(1)求证：$\triangle BCD\cong\triangle FCE$；
(2)若$EF// CD$,求$\angle BDC$的度数。

答案：
(1)$\because$将线段$CD$绕点$C$按顺时针方向旋转$90^{\circ}$后得$CE,\therefore CD = CE,\angle DCE = B90^{\circ}$。
$\because \angle ACB = 90^{\circ}$，
$\therefore \angle ACB-\angle DCA=\angle DCE-\angle DCA$，
即$\angle BCD=\angle FCE$。
在$\triangle BCD$和$\triangle FCE$中，$\begin{cases}CB = CF,\\\angle BCD=\angle FCE,\\CD = CE,\end{cases}$
$\therefore \triangle BCD\cong \triangle FCE(SAS)$。
(2)由
(1)可知$\triangle BCD\cong \triangle FCE$，
$\therefore \angle BDC=\angle E,\angle BCD=\angle FCE$。
$\because EF// CD,\angle DCE = 90^{\circ}$，
$\therefore \angle E = 180^{\circ}-\angle DCE = 90^{\circ}$，
$\therefore \angle BDC = 90^{\circ}$。
知识拓展 本题考查了全等三角形的判定和性质、同角的余角相等、旋转的性质、平行线的性质，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具。在判定三角形全等时，关键是选择恰当的判定条件。

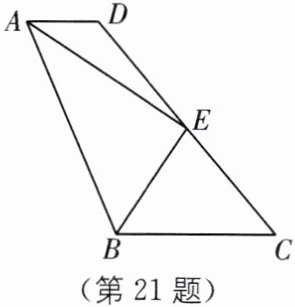
21. 如图,$AD// BC$,$EA$、$EB分别平分\angle DAB$、$\angle CBA$,$CD过点E$,求证：$AB = AD + BC$。

答案： 在$AB$上取点$F$，使$AF = AD$，连接$FE$，
易知$\triangle ADE\cong \triangle AFE(SAS),\therefore \angle ADE=\angle AFE$。
$\because AD// BC,\therefore \angle ADE+\angle BCE = 180^{\circ}$。
又$\angle AFE+\angle BFE = 180^{\circ}$，
$\therefore \angle ECB=\angle BFE$，
$\therefore \triangle FBE\cong \triangle CBE(AAS)$，
$\therefore BF = BC,\therefore AB = AF + BF = AD + BC$。