第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如果两个图形全等,那么这两个图形必定是(
A.形状大小均相同
B.形状相同,但大小不同
C.大小相同,但形状不同
D.形状大小均不相同
A
)。A.形状大小均相同
B.形状相同,但大小不同
C.大小相同,但形状不同
D.形状大小均不相同
答案:
A
2. 如图,$\triangle ABC\cong\triangle ADE$,$AB = AD$,$AC = AE$。若$\angle B = 30^{\circ}$,$\angle E = 100^{\circ}$,$\angle CAD = 20^{\circ}$,则$\angle BAD$等于(
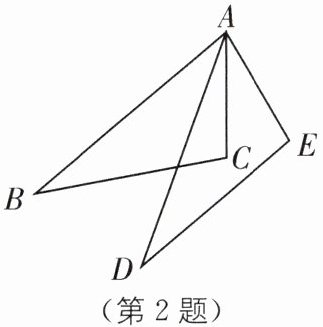
A.$20^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$50^{\circ}$
C
)。
A.$20^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$50^{\circ}$
答案:
C
3. 如图,在$\triangle ABC和\triangle DEC$中,已知$AB = DE$,还需添加两个条件才能使$\triangle ABC\cong\triangle DEC$,不能添加的一组条件是(
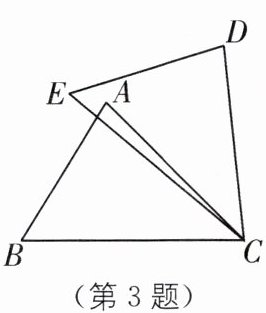
A.$BC = EC$,$\angle B = \angle E$
B.$BC = EC$,$AC = DC$
C.$BC = DC$,$\angle A = \angle D$
D.$\angle B = \angle E$,$\angle A = \angle D$
C
)。
A.$BC = EC$,$\angle B = \angle E$
B.$BC = EC$,$AC = DC$
C.$BC = DC$,$\angle A = \angle D$
D.$\angle B = \angle E$,$\angle A = \angle D$
答案:
C
4. 工人师傅常用角尺平分一个任意角。做法如下:如图,$\angle AOB$是一个任意角,在边$OA$、$OB上分别取OM = ON$,移动角尺,使角尺两边相同的刻度分别与$M$、$N$重合。过角尺顶点$C作射线OC$。由做法得$\triangle MOC\cong\triangle NOC$的依据是(
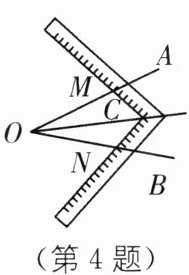
A.AAS
B.SAS
C.ASA
D.SSS
D
)。
A.AAS
B.SAS
C.ASA
D.SSS
答案:
D
5. 如图,在$\angle AOB$中,$OM平分\angle AOB$,$MA\perp OA$,垂足为$A$,$MB\perp OB$,垂足为$B$。若$\angle MAB = 20^{\circ}$,则$\angle AOB$的度数为(

A.$20^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$40^{\circ}$
D
)。
A.$20^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$40^{\circ}$
答案:
D
6. 如图,在$\triangle ABC$中,$AB = AC$,点$D为BC$上一点,$BF = CD$,$CE = BD$,那么$\angle EDF$等于(
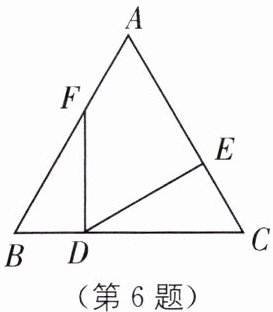
A.$90^{\circ}-\angle A$
B.$90^{\circ}-\frac{1}{2}\angle A$
C.$180^{\circ}-\angle A$
D.$45^{\circ}-\frac{1}{2}\angle A$
B
)。
A.$90^{\circ}-\angle A$
B.$90^{\circ}-\frac{1}{2}\angle A$
C.$180^{\circ}-\angle A$
D.$45^{\circ}-\frac{1}{2}\angle A$
答案:
B
7. 如图,$\angle E = \angle F = 90^{\circ}$,$\angle B = \angle C$,$AE = AF$,下列结论:①$EM = FN$;②$CD = DN$;③$\angle FAN = \angle EAM$;④$\triangle ACN\cong\triangle ABM$。其中正确的有(
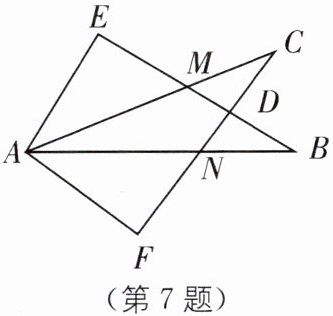
A.1个
B.2个
C.3个
D.4个
C
)。
A.1个
B.2个
C.3个
D.4个
答案:
C
8. 如图,在$\triangle AFD和\triangle CEB$中,点$A$、$E$、$F$、$C$在同一条直线上,有下列四个论断:①$AD = CB$;②$AD// BC$;③$AE = CF$;④$\angle D = \angle B$。用其中的三个作为条件,不能得到$\triangle ADF\cong\triangle CBE$的三个条件的序号是(
A.①②③
B.①②④
C.②③④
D.①③④
D
)。A.①②③
B.①②④
C.②③④
D.①③④
答案:
D
查看更多完整答案,请扫码查看


