《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

18. 如图,$OP= 1$,过点P作$PP_{1}⊥OP且PP_{1}= 1$,得$OP_{1}= \sqrt {2}$；再过点$P_{1}作P_{1}P_{2}⊥OP_{1}且P_{1}P_{2}= 1$,得$OP_{2}= \sqrt {3}$；又过点$P_{2}作P_{2}P_{3}⊥OP_{2}且P_{2}P_{3}= 1$,得$OP_{3}= 2$；….依此法继续作下去,得$OP_{2024}= $45.

答案： 45

19. 已知a为实数,求代数式$\sqrt {a+2}-\sqrt {8-4a}+\sqrt {-a^{2}}$的值.

答案： 原式=−$\sqrt{2}$

20. 已知a的立方根是3,b的算术平方根是4,一个正数c的两个平方根分别是$d+1和2d-7$,求$a+b-2c$的平方根.

答案：
∵a的立方根是3，b的算术平方根是4，
∴a=27，b=16。
∵一个正数c的两个平方根分别是d+1和2d−7，
∴d+1+2d−7=0，解得d=2。
∴c=(2+1)²=9。
∴a+b−2c=27+16−2×9=25。
∴a+b−2c的平方根是±5。

21. “欲穷千里目,更上一层楼”,说的是登得高看得远,若观测点的高度为h,观测者视线能达到的最远距离为d,则$d= \sqrt {2hR}$,其中R是地球半径(通常取6400km).如图,小丽站在海边一块岩石上,眼睛离海平面的高度h为20m,她观测到远处一艘船刚露出海平面,求此时d的值.

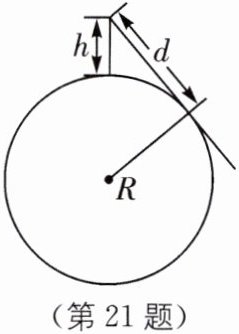
答案： 由R=6400km，h=0.02km，得d=$\sqrt{2hR}$=$\sqrt{2×0.02×6400}$=$\sqrt{256}$=16 (km)，故此时d的值为16km。

22. 如图,有人在岸上点C的地方,用绳子拉船靠岸.开始时,绳长$CB= 5m$,拉动绳子将船身朝岸边行驶了2m到点D后,绳长$CD= \sqrt {13}m$,求岸上点C离水面的高度CA.

答案： 设AD为xm，由题意，得($\sqrt{13}$)²−x²=5²−(x+2)²，解得x=2。AC=$\sqrt{5²−4²}$=3m。故岸上点C离水面的高度AC为3m。