第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD= BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED= AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是(
A.边角边
B.角边角
C.边边边
D.边边角
B
).A.边角边
B.角边角
C.边边边
D.边边角
答案:
B
2. 如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(
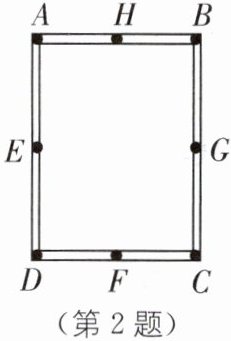
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
B
).
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
答案:
B
3. 建成具有全球影响力的“工程机械之都、汉文化名城”是徐州市2035远景目标,下列四个数字图形中,中心对称图形共有(

A.1个
B.2个
C.3个
D.4个
C
).
A.1个
B.2个
C.3个
D.4个
答案:
C [解析]中心对称图形,即把一个图形绕一个点旋转$180^{\circ }$后能和原来的图形重合,所以数字图形中的“2”“0”“5”均为中心对称图形,故中心对称图形共有3个.故选C.
4. 近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多. 为了解南迁到该区域某湿地的A种候鸟的情况,从中捕捉40只,戴上识别卡并放回;经过一段时间后观察发现,200只A种候鸟中有10只佩有识别卡,由此估计该湿地约有______只A种候鸟.
[答案]:
[答案]:
800
答案:
800
5. 如图是一种单肩包,其背带由双层部分、单层部分和调节扣构成. 小文购买时,售货员演示通过调节扣加长或缩短单层部分的长度,可以使背带的长度(单层部分与双层部分长度的和,其中调节扣所占长度忽略不计)加长或缩短,设双层部分的长度为x cm,单层部分的长度为y cm. 经测量,得到表中数据.
|双层部分长度x/cm|2|8|14|20|
|单层部分长度y/cm|148|136|124|112|
(1)根据表中数据规律,求出y与x的函数关系式;
(2)按小文的身高和习惯,背带的长度调为130 cm时为最佳背带长. 请计算此时双层部分的长度;
(3)设背带的长度为L cm,求L的取值范围.

|双层部分长度x/cm|2|8|14|20|
|单层部分长度y/cm|148|136|124|112|
(1)根据表中数据规律,求出y与x的函数关系式;
(2)按小文的身高和习惯,背带的长度调为130 cm时为最佳背带长. 请计算此时双层部分的长度;
(3)设背带的长度为L cm,求L的取值范围.

答案:
(1)设y与x的函数关系式为$y=kx+b$,
由题意,得$\left\{\begin{array}{l} 148=2k+b\\ 136=8k+b\end{array}\right. $,解得$\left\{\begin{array}{l} k=-2\\ b=152\end{array}\right. $,
$\therefore$y与x的函数关系式为$y=-2x+152$.
(2)由题意,得$\left\{\begin{array}{l} x+y=130\\ y=-2x+152\end{array}\right. $,
解得$\left\{\begin{array}{l} x=22\\ y=108\end{array}\right. $,
$\therefore$双层部分的长度为22cm.
(3)由题意得,当$x=0$时,$y=152$,
当$y=0$时,$x=76$,$\therefore 76\leqslant L\leqslant 152$.
(1)设y与x的函数关系式为$y=kx+b$,
由题意,得$\left\{\begin{array}{l} 148=2k+b\\ 136=8k+b\end{array}\right. $,解得$\left\{\begin{array}{l} k=-2\\ b=152\end{array}\right. $,
$\therefore$y与x的函数关系式为$y=-2x+152$.
(2)由题意,得$\left\{\begin{array}{l} x+y=130\\ y=-2x+152\end{array}\right. $,
解得$\left\{\begin{array}{l} x=22\\ y=108\end{array}\right. $,
$\therefore$双层部分的长度为22cm.
(3)由题意得,当$x=0$时,$y=152$,
当$y=0$时,$x=76$,$\therefore 76\leqslant L\leqslant 152$.
查看更多完整答案,请扫码查看


