《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

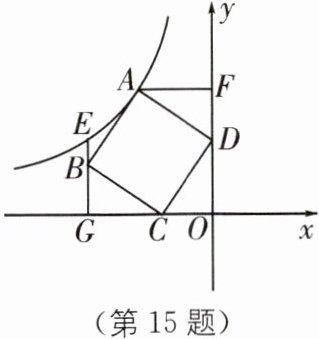
15. 如图(1),在正方形$ABCD$中,$C(-3,0)$、$D(0,4)$。过点$A作AF\perp y轴于点F$,过点$B作x轴的垂线交过点A的反比例函数的图像于点E$,交$x轴于点G$。
(1)求证：$\triangle CDO\cong \triangle DAF$；
(2)求点$E$的坐标。

答案：
(1)$\because C(-3,0)$、$D(0,4)$，$\therefore OC=3$，$OD=4$．
∵四边形$ABCD$为正方形，$\therefore AD=CD$，$∠ADC=90^{\circ }$．$\therefore ∠ADF+∠CDO=90^{\circ }$．$\because AF⊥y$轴，$\therefore ∠AFD=90^{\circ }$．$\therefore ∠ADF+∠DAF=90^{\circ }$．$\therefore ∠DAF=∠CDO$．在$\triangle CDO$和$\triangle DAF$中，$\left\{\begin{array}{l} ∠DOC=∠AFD,\\ ∠CDO=∠DAF,\\ CD=DA,\end{array}\right. $$\therefore \triangle CDO\cong \triangle DAF(AAS)$．
(2)点$E$的坐标为$(-7,4)$．

16. 工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到$800^{\circ}C$,然后停止煅烧进行锻造操作。经过8min时,材料温度降为$600^{\circ}C$,煅烧时,温度$y(^{\circ}C)与时间x(min)$成一次函数关系；锻造时,温度$y(^{\circ}C)与时间x(min)$成反比例关系(如图所示),已知该材料初始温度是$32^{\circ}C$。
(1)分别求出材料煅烧和锻造时$y与x$的函数关系式,并且写出自变量$x$的取值范围。
(2)根据工艺要求,当材料温度低于$480^{\circ}C$时,须停止操作,那么锻造的操作时间有多长？

答案：
(1)材料煅烧时，$y$与$x$的函数关系式为$y=128x+32(0≤x≤6)$；材料锻造时，$t_{终}=\frac {4800}{32}=150min$，所以$y$与$x$的函数关系式为$y=\frac {4800}{x}(6＜x≤150)$．
(2)4min