《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

20. 已知$|a - b + 1|与\sqrt{a + 2b + 4}$互为相反数,求$(a - b)^{2024}$的值.

答案： 由题意，得$\begin{cases}a - b + 1 = 0,\\a + 2b + 4 = 0,\end{cases}$解得$\begin{cases}a = - 2,\\b = - 1.\end{cases}$ 所以$(a - b)^{2024}=[-2-(-1)]^{2024}=(-1)^{2024}=1$.

21. 已知$a$、$b$、$c$为三角形的三边,化简：$\sqrt{(a + b - c)^2} + \sqrt{(b - c - a)^2} + \sqrt{(b + c - a)^2}$.

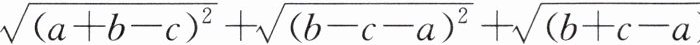
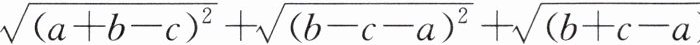
答案： 原式$=a + b - c + a + c - b + b + c - a = a + b + c$.

22. 中考新考法 满足结论的条件开放 已知一个三角形的三边长分别为$3\sqrt{\frac{x}{3}}$、$\frac{1}{2}\sqrt{12x}$、$\frac{3}{4}x\sqrt{\frac{4}{3x}}$.
(1)求它的周长；(要求结果化简)
(2)请你给出一个适当的$x$值,使它的周长为整数,并求出此时三角形周长的值.

答案：
(1)$3\sqrt{\frac{x}{3}}+\frac{1}{2}\sqrt{12x}+\frac{3}{4}x\sqrt{\frac{4}{3x}}=\sqrt{3x}+\sqrt{3x}+\frac{\sqrt{3x}}{2}=\frac{5\sqrt{3x}}{2}$.
(2)当$x = 12$时，周长为$\frac{5\sqrt{3x}}{2}=15$（答案不唯一）。

23. 已知$\sqrt{a} + \sqrt{b} = \sqrt{3} + \sqrt{2}$,$\sqrt{ab} = \sqrt{6} - \sqrt{3}$,求$a + b$的值.

答案： $5 + 2\sqrt{3}$

24. 中考新考法 归纳一般结论 观察下列等式：
第1个等式：$a_1 = \frac{1}{1 + \sqrt{2}} = \sqrt{2} - 1$；
第2个等式：$a_2 = \frac{1}{\sqrt{2} + \sqrt{3}} = \sqrt{3} - \sqrt{2}$；
第3个等式：$a_3 = \frac{1}{\sqrt{3} + 2} = 2 - \sqrt{3}$；
第4个等式：$a_4 = \frac{1}{2 + \sqrt{5}} = \sqrt{5} - 2$；…
按上述规律,回答以下问题：
(1)请写出第$n$个等式：$a_n = $$\frac{1}{\sqrt{n}+\sqrt{n + 1}}=\sqrt{n + 1}-\sqrt{n}$；
(2)求$a_1 + a_2 + a_3 + … + a_n$。$\sqrt{n + 1}-1$

答案：
(1)$\frac{1}{\sqrt{n}+\sqrt{n + 1}}=\sqrt{n + 1}-\sqrt{n}$
(2)$\sqrt{n + 1}-1$