第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10. 一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗,每次随机摸出一颗珠子,放回摇匀后再摸,通过多次试验发现摸到白珠子的频率稳定在0.3左右,则盒子中黑珠子可能有
14
颗.
答案:
14
11. 某同学遇到一道不会做的选择题,在四个选项中有且只有一个是正确的,则他选对的概率是
$\frac {1}{4}$
.
答案:
$\frac {1}{4}$
12. 如图表示三个袋中分别装进只有颜色不同的5个球,从中抽出一个,请你按照摸到红球的可能性由大到小,把序号进行排列
②>③>①
.
答案:
②>③>①
13. 一副扑克牌中抽出5张黑桃、4张梅花、6张红桃,现从中抽取m张,要求3种花色的牌都有是必然事件,那么m的最小值是
12
.
答案:
12
14. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有80个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、白色球的频率分别稳定在10%和60%,则口袋中黑色球的个数很可能是
24
个.
答案:
24
15. 甲、乙两人玩扑克牌游戏,游戏规则是:从牌面数字分别为5、6、7的三张扑克牌中随机抽取一张,放回后再随机抽取一张,若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽取的两张牌面数字的积为偶数,则乙获胜.这个游戏
不公平
.(填“公平”或“不公平”)
答案:
不公平
16. 某射手在相同条件下进行射击训练,结果如下表所示:
|射击次数n|10|20|50|100|200|500|
|击中靶心次数m|9|19|44|91|178|450|
|击中靶心频率|0.90|0.95|0.88|0.91|0.89|0.90|
试根据该表,估计这名射手射击一次,击中靶心的概率约为
|射击次数n|10|20|50|100|200|500|
|击中靶心次数m|9|19|44|91|178|450|
|击中靶心频率|0.90|0.95|0.88|0.91|0.89|0.90|
试根据该表,估计这名射手射击一次,击中靶心的概率约为
0.90
.
答案:
0.90
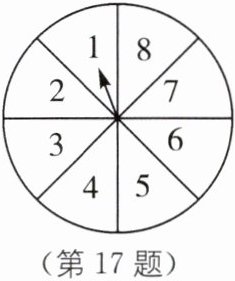
17. 如图,转盘被平均分成8份,自由转动转盘,下列事件是必然事件、不可能事件还是随机事件?根据你的经验,将这些事件发生的可能性按从小到大的顺序排列.
①转盘停止后指针指向10;
②转盘停止后指针指向1;
③转盘停止后指针指向的数大于1;
④转盘停止后指针指向的不是奇数就是偶数;
⑤转盘停止后指针指向的数是偶数.
①转盘停止后指针指向10;
②转盘停止后指针指向1;
③转盘停止后指针指向的数大于1;
④转盘停止后指针指向的不是奇数就是偶数;
⑤转盘停止后指针指向的数是偶数.

答案:
必然事件:④;不可能事件:①;随机事件:②③⑤;发生的可能性按从小到大的顺序排列是①②⑤③④.
|转动转盘的次数n|100|150|200|500|800|1000|
|落在“铅笔”的频数m|68|111|136|345|564|701|
|落在“铅笔”的频率$\frac {m}{n}$|
(2)请你估计,当n很大时,频率会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的可能性大约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少度?
|落在“铅笔”的频数m|68|111|136|345|564|701|
|落在“铅笔”的频率$\frac {m}{n}$|
0.68
|0.74
|0.68
|0.69
|0.705
|0.701
|(2)请你估计,当n很大时,频率会接近多少?
由上可知,当n很大时,频率将接近0.70.
(3)假如你去转动该转盘一次,你获得铅笔的可能性大约是多少?
假如你去转动该转盘一次,你获得铅笔的可能性大约是0.7.
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少度?
$360^{\circ }×0.7=252^{\circ }$,在该转盘中,表示“铅笔”区域的扇形的圆心角约是$252^{\circ }$.
答案:
(1)0.68 0.74 0.68 0.69 0.705 0.701
(2)由上可知,当n很大时,频率将接近0.70.
(3)假如你去转动该转盘一次,你获得铅笔的可能性大约是0.7.
(4)$360^{\circ }×0.7=252^{\circ }$,在该转盘中,表示“铅笔”区域的扇形的圆心角约是$252^{\circ }$.
(1)0.68 0.74 0.68 0.69 0.705 0.701
(2)由上可知,当n很大时,频率将接近0.70.
(3)假如你去转动该转盘一次,你获得铅笔的可能性大约是0.7.
(4)$360^{\circ }×0.7=252^{\circ }$,在该转盘中,表示“铅笔”区域的扇形的圆心角约是$252^{\circ }$.
查看更多完整答案,请扫码查看


