《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

11. 为了绿化学校,需移植草皮到操场,若矩形操场的长比宽多14m,而面积是$3200m^{2}$,则绿化后操场上草皮的长为64m,宽为50m。

答案： $64$ $50$

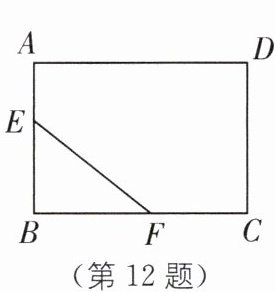
12. 如图,在矩形$ABCD$中,$AB= 6$,$BC= 8$,点$E从点A$出发,以1个单位每秒的速度向$B$移动,同时,点$F从点B$出发,以2个单位每秒的速度向$C$移动,1秒后$\triangle EBF$的面积为5个平方单位。

答案： $1$

13. 某百货大楼服装柜在销售中发现：某品牌童装平均每天可售出20件,每件盈利40元。为了迎接“元旦”,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现：如果每件童装降价1元,那么平均每天就可多售出2件,现设降价$x$元,日销售量为$y$件,每天的销售总利润为$W$元。
(1)用含$x的代数式表示y$。
(2)当$x= 3$时,求$W$的值。
(3)要想销售这种童装平均每天能盈利1200元,那么每件童装应降价多少元？

答案：
(1)$y = 20 + 2x$.
(2)$W = (40 - x)(20 + 2x)$，
当$x = 3$时，$W = 962$.
(3)依题意，得$(40 - x)\cdot(20 + 2x) = 1200$.
解得$x_1 = 10$，$x_2 = 20$，均符合题意，
即每件童装应降低$10$元或$20$元.

14. 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门。所围矩形猪舍的长、宽分别为多少时,猪舍面积为$80m^{2}$？

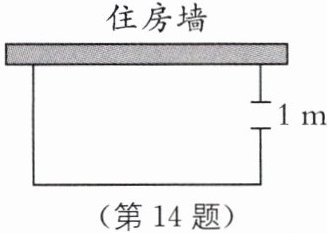
答案： 设矩形猪舍垂直于住房墙的一边长为$x\ \text{m}$，则矩形猪舍的另一边为$(26 - 2x)\ \text{m}$.
根据题意，得$x(26 - 2x) = 80$，
解得$x_1 = 5$，$x_2 = 8$.
当$x = 5$时，$26 - 2x = 16 ＞ 12$(舍去)；
当$x = 8$时，$26 - 2x = 10 ＜ 12$.
因此所建矩形猪舍的长为$10\ \text{m}$，宽为$8\ \text{m}$.

15. 新情境 大气环境保护 某厂工业废气年排放量为400万立方米,为改善某市的大气环境质量,决定分二期投入治理,使废气的年排放量减少到256万立方米,如果每期治理中废气减少的百分率相同。
(1)求每期减少的百分率是多少。
(2)预计第一期治理中每减少1万立方米废气需投入3万元,第二期治理中每减少1万立方米废气需投入4.5万元,问两期治理完成后需投入多少万元？

答案：
(1)设每期减少的百分率是$x$，
根据题意得$400(1 - x)^2 = 256$，
解得$x_1 = 0.2$，$x_2 = 1.8$(舍去)，
所以每期减少的百分率为$20\%$.
(2)根据题意得，$400×0.2×3 = 240$(万元)，
$(400 - 400×0.2)×0.2×4.5 = 288$(万元)，
$\therefore 240 + 288 = 528$(万元).
故两期治理完成后需要投入$528$万元.