《2025年实验班提优训练暑假衔接版八升九年级数学苏科版》

20. 如图,在等边三角形$ABC$中,$AC= 6$,点$O在AC$上,且$AO= 2$,点$P是AB$上一动点,连接$OP$,将线段$OP绕点O逆时针旋转60^{\circ}得到线段OD$,要使点$D恰好落在BC$上,则$AP$的长是4。

答案： 4

21. 如图,已知$\triangle ABC$的三个顶点在格点上。
(1)作出与$\triangle ABC关于x轴对称的图形\triangle A_1B_1C_1$；
(2)求出$\triangle A_1B_1C_1$的面积。

答案：

(1)如图所示,$\triangle A_1B_1C_1$即为所求.

(2)$\triangle A_1B_1C_1$的面积为$4-\frac{1}{2}×1×1-2×\frac{1}{2}×1×2=\frac{3}{2}$.

22. 一个正数的平方根分别是$2a+5和2a-1$,$b-30的立方根是-3$,求：
(1)$a$、$b$的值；
(2)$a+b$的算术平方根。

答案：
(1)由题意可知$(2a + 5)+(2a - 1)=0$,$b - 30 = (-3)^3 = -27$,
解得$a = -1$,$b = 3$.
(2)$\because a + b = -1 + 3 = 2$,
$\therefore a + b$的算术平方根是$\sqrt{2}$.
方法诠释 本题考查了平方根、算术平方根、立方根的定义,解题的关键是正确理解算术平方根的定义,本题属于基础题型.

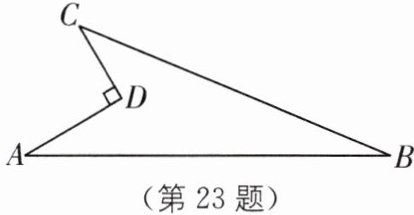
23. 如图,已知某开发区有一块四边形空地$ABCD$,现计划在该空地上种植草皮,经测量$\angle ADC= 90^{\circ}$,$CD= 6m$,$AD= 8m$,$BC= 24m$,$AB= 26m$,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱？

答案：
如图,连接$AC$,

在$Rt\triangle ACD$中,$AC^2 = CD^2 + AD^2 = 6^2 + 8^2 = 10^2(m^2)$,
在$\triangle ABC$中,$AB^2 = 26^2m^2$,$BC^2 = 24^2m^2$,
而$10^2 + 24^2 = 26^2$,即$AC^2 + BC^2 = AB^2$,
$\therefore\angle ACB = 90^{\circ}$.
$S_{四边形ABCD}=S_{\triangle ACB}-S_{\triangle ACD}$
$=\frac{1}{2}AC\cdot BC-\frac{1}{2}AD\cdot CD$
$=\frac{1}{2}×10×24-\frac{1}{2}×8×6$
$=96(m^2)$.
所以需费用$96×200 = 19200$(元).

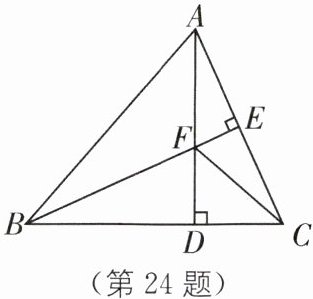
24. 如图,在$\triangle ABC$中,$AB= BC$,$BE \perp AC于点E$,$AD \perp BC于点D$,$\angle BAD= 45^{\circ}$,$AD与BE交于点F$,连接$CF$。
(1)求证：$BF= 2AE$；
(2)若$CD= \sqrt{2}$,求$AD$的长。

答案：
(1)$\because AD\perp BC$,$\angle BAD = 45^{\circ}$,
$\therefore\triangle ABD$是等腰直角三角形.
$\therefore AD = BD$.
$\because BE\perp AC$,$AD\perp BC$,
$\therefore\angle CAD+\angle ACD = 90^{\circ}$,$\angle CBE+\angle ACD = 90^{\circ}$.
$\therefore\angle CAD = \angle CBE$.
在$\triangle ADC$和$\triangle BDF$中,
$\begin{cases}\angle CAD=\angle FBD,\\AD=BD,\\\angle ADC=\angle BDF=90^{\circ},\end{cases}$
$\therefore\triangle ADC\cong\triangle BDF(ASA)$.
$\therefore BF = AC$.
$\because AB = BC$,$BE\perp AC$,
$\therefore AC = 2AE$.
$\therefore BF = 2AE$.
(2)$AD = 2+\sqrt{2}$.