《2025年从课本到奥数同步练六年级数学下册苏教版》

1. 填空。
(1) 在一个比例中，两个比的比值都是1.5，两个外项分别是12和45，这个比例是(　　　　　　)或(　　　　　　)。
(2) 在比例12：45 = 8：30中，如果第一个比的后项增加15，那么第二个比的前项应该减少(　　　)才能使比例成立。
(3) 若5m = 4n(m、n均不为0)，则m：n = (　　　)：(　　　)。
(4) 若甲数的$\frac{5}{7}$与乙数的$\frac{4}{5}$相等(甲、乙两数均不为0)，甲数：乙数 = (　　　)：(　　　)。
(5) 给3、5、9再配上一个数，组成比例，这个数最大是(　　　)，最小是(　　　)，还可能是(　　　)。

答案：
(1) 12 : 8 = 67.5 : 45 45 : 30 = 18 : 12
(2) 2
(3) 4 5
(4) 28 25
(5) 15 $\frac{5}{3}$ $\frac{27}{5}$

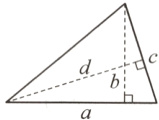
(1) 如图，三角形a边上的高为b，c边上的高为d。根据这些信息，下面式子中(　　　)不成立。
A. a：c = d：b
B. a：c = b：d
C. $\frac{a}{d}=\frac{c}{b}$

答案：
(1) B

(2) 如果平行四边形相邻两条边上的高分别为12和18，那么这两条边的比是(　　　)。
A. 2：3
B. 3：2
C. 无法确定

答案：  
(2) B

例 甲、乙、丙三人进行200米赛跑(假设他们的速度不变)，当甲到达终点时，乙离终点还有20米，丙离终点还有25米。当乙到达终点时，丙离终点还有多少米?

答案： 分析与解答 根据题意，当甲跑了200米时，乙跑了(200 - 20)米，丙跑了(200 - 25)米，此时他们用的时间相同，速度比等于路程比，所以乙、丙的速度比为(200 - 20)：(200 - 25)。由于乙、丙的速度不变，当时间相同时速度比也就是路程比。当乙跑了200米时就能根据路程比求出丙跑的路程。
(200 - 20)：(200 - 25)= 36：35
200 - 200×$\frac{35}{36}=\frac{50}{9}$(米)
小窍门 比例是表示两个相关联的量之间的一种关系。在解决相关行程问题时，要注意相同的时间内，路程比即速度比。本题就是通过甲到达终点时乙、丙所行路程比算出乙、丙的速度比，进而解决问题。

1. 甲、乙、丙三辆电动玩具车进行400米测试。当丙到达终点时，乙跑了320米，甲距终点还有100米。如果甲、乙速度不变，那么当乙到达终点时，甲距终点还有多少米?

答案： 1. 320 : (400 - 100) = 16 : 15 (400 - 320)÷16×15 = 75(米) 100 - 75 = 25(米) 【提示：在相同时间内，路程比等于速度比。】

2. 一座钟每小时要比标准时间快3分钟，早上8时将这座钟时间调准，当钟面显示下午3时时，标准时间是几时几分?

答案： 2. 60 : (60 + 3) = 60 : 63 = 20 : 21 下午3时 = 15时 (15 - 8)×$\frac{20}{21}$ = $\frac{20}{3}$(小时) $\frac{20}{3}$时 = 6时40分 8时 + 6时40分 = 14时40分 【提示：标准时间走1小时(60分钟)，错误时间走60 + 3 = 63(分钟)，相同时间内，标准时间与错误时间的比是60 : 63，根据时间比解决问题。】