《2025年从课本到奥数同步练六年级数学下册苏教版》

1. 一个圆柱的高是5分米，侧面积是62.8平方分米，它的底面积是( )平方分米，体积是( )立方分米。

答案： 4π(或12.56) 20π(或62.8)

2. 等底等高的一个圆柱和一个圆锥，它们的体积和是96立方厘米，体积差是( )立方厘米。

答案： 48

3. 一个圆锥的底面周长是18.84厘米，高是5厘米，从顶点沿高把它切成相等的两半，表面积增加了( )平方厘米。这个圆锥的体积是( )立方厘米。

答案： 30 15π(或47.1)

4. 一个圆锥形铅块，底面半径和高都是12厘米，若把它熔铸成与它等高的圆柱，则圆柱的底面积是( )平方厘米；一个圆柱形铅块，底面半径和高都是12厘米，若把它熔铸成与它等高的圆锥，则圆锥的底面积是( )平方厘米。

答案： 48π(或150.72) 432π(或1356.48) [提示:圆柱和圆锥体积相等，高相等，底面积的比是1:3。]

1. 把一个底面半径和高都是2分米的圆柱沿底面半径分成若干等份，切拼成一个近似的长方体，表面积增加( )平方分米。
A. 4 B. 2π C. 8

答案： C

2. 将24个圆锥形铁块熔铸成等底等高的圆柱，可以熔铸( )个。
A. 8 B. 36 C. 72

答案： A

3. 把一个棱长为4分米的正方体木块削成一个最大的圆柱。圆柱的体积正好是正方体体积的( )。
A. $\frac{1}{3}$ B. 21.5% C. 78.5%

答案： C

4. 底面积相等的圆柱和圆锥，它们的体积比是2：1，圆锥的高是9厘米，圆柱的高是( )厘米。
A. 3 B. 6 C. 18

答案： B

1. 如图，ABCD是直角梯形，以CD为轴将这个直角梯形旋转一周，得到一个旋转体。这个旋转体的体积是多少立方厘米？

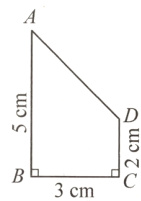
答案： $\pi\times3^{2}\times5 - \frac{1}{3}\times\pi\times3^{2}\times(5 - 2)=36\pi$(立方厘米)(或113.04立方厘米)

2. 一个圆锥形沙堆，底面周长是18.84米，高是2米。把这堆沙均匀地铺在宽10米的公路上，若铺0.12米厚，则可铺多少米长？(π取3.14)

答案： 18.84÷3.14 = 6(米) $\frac{1}{3}\times3.14\times(6\div2)^{2}\times2 = 18.84$(立方米) 18.84÷(10×0.12)=15.7(米)

3. 在一个底面直径是40厘米的圆柱形容器里，有一个底面直径是20厘米的圆锥形铁块完全浸没在水中。当把铁块从圆柱形容器里取出时，容器里的水面下降了1厘米。这个圆锥形铁块的高是多少厘米？

答案： $\pi\times(40\div2)^{2}\times1 = 400\pi$(立方厘米) 400π×3÷[$\pi\times(20\div2)^{2}$]=12(厘米)

4. 一个高为20厘米的圆柱，若高增加2厘米，则表面积增加62.8平方厘米。原来圆柱的体积是多少立方厘米？

答案： 62.8÷2 = 31.4(厘米) 31.4÷3.14÷2 = 5(厘米) $\pi\times5^{2}\times20 = 500\pi$(立方厘米)(或1570立方厘米)