《2025年从课本到奥数同步练六年级数学下册苏教版》

1. 填空。
（1）一个圆锥的体积是80立方厘米，高是24厘米，与它等底的圆柱的体积比它多40立方厘米。这个圆柱的高是(　　　)厘米。
（2）一个圆锥和一个圆柱体积相等，底面半径的比是3∶2。圆锥的高是12厘米，圆柱的高是(　　　)厘米。

答案：
(1)12　
(2)9　[提示:圆锥和圆柱体积的比是1:1,底面半径的比是3:2,即底面积的比是3²:2²=9:4,高的比是(1×3÷9):(1÷4)=4:3。]

2.（1）将一个底面直径20厘米、高12厘米的圆锥形金属块全部浸没在底面直径是40厘米的圆柱形水槽中，水槽水面会升高多少厘米？
（2）将一个底面直径是20厘米的圆锥形金属块全部浸没在底面直径是40厘米的圆柱形水槽中，水面上升1.5厘米。圆锥形金属块的高是多少厘米？

答案：
(1)$\frac{1}{3}×\pi×(20÷2)^{2}×12 = 400\pi$(立方厘米)
$400\pi÷[\pi×(40÷2)^{2}]=1$(厘米)
(2)$\pi×(40÷2)^{2}×1.5 = 600\pi$(立方厘米)
$600\pi×3÷[\pi×(20÷2)^{2}]=18$(厘米)
[提示:已知圆锥的体积求底面积或高，先把圆锥的体积乘3转化为等底等高的圆柱，再求底面积或高。]

3. 把一个圆锥沿高切开，得到相同的两部分，每部分的横截面是18平方厘米。如果圆锥的高是3厘米，它的底面积是多少平方厘米？体积是多少立方厘米？

答案： 18×2÷3 = 12(厘米) 底面积：$\pi×(12÷2)^{2}=36\pi$(平方厘米)(或113.04平方厘米) 体积：$\frac{1}{3}×36\pi×3 = 36\pi$(立方厘米)(或113.04立方厘米)

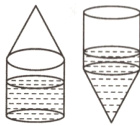
例 如图，一个下面是圆柱、上面是圆锥的容器。圆柱的高是14厘米，圆锥的高是12厘米。容器内水面的高是9厘米，当将这个容器倒过来时，从圆锥的顶点到水面的高是多少厘米？

答案： 分析与解答 无论正放还是倒放，水的体积不变。圆柱和圆锥底面积相等，倒放时，圆锥里装水的高度只相当于圆柱里装水高度的$\frac{1}{3}$，圆锥里水的高是12厘米，对应圆柱里水的高度是12÷3 = 4(厘米)。圆柱里水的高度是9 - 4 = 5(厘米)，整个水面的高度是5 + 12 = 17(厘米)。
小窍门 解答这类问题时，要善于抓住“等积”这一个条件，把一种形体(或几种形体)变形为另一种形体(或几种形体)，它们之间的体积(或面积)不变。

1. 在一个底面积为314平方厘米的圆柱形容器中放入等底等高的一个圆柱形物体和一个圆锥形物体，水面上升了7厘米，圆柱形物体有$\frac{2}{5}$露出水面，圆锥形物体完全浸没在水中。圆锥形物体的体积是多少立方厘米？

答案： 1.$1 - \frac{2}{5}=\frac{3}{5}$ $(1×1×\frac{3}{5}):(1×1×\frac{1}{3}) = 9:5$
314×7 = 2198(立方厘米) $2198×\frac{5}{9 + 5}=785$(立方厘米)
[提示:因为圆锥形物体完全浸没在水中，所以圆锥形物体的体积转化成了水的体积。因为圆柱形物体有$\frac{2}{5}$露出水面，所以圆柱形物体体积的$(1 - \frac{2}{5})$转化成了水的体积。先求出圆柱形物体和圆锥形物体转化成水的体积比，然后求出水上升的体积，再按比例分配求出圆锥形物体的体积。]

2. 甲、乙两个圆柱形容器，底面积的比是4∶3，甲容器里的水深3厘米，乙容器里没有水。现往两个容器里注入同样多的水，直到水深相等，这时水深多少厘米？

答案： 2.解:设这时水深x厘米。$4(x - 3)=3x$ $x = 12$
[提示:根据注入水的体积相等列出等式，甲注入水的体积应该是底面积×(这时水深 - 3)。]