2025年从课本到奥数同步练六年级数学下册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年从课本到奥数同步练六年级数学下册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
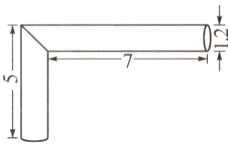
1. 如图是一种燃气排气管,做这样一个排气管至少需要多少平方分米的铁皮?(单位:分米)

答案:
$\pi\times1.2\times(5 + 7)=14.4\pi$(平方分米)(或 45.216 平方分米)【提示:这个排气管若沿接头处分开,旋转后即可拼接成一个圆柱,排气管没有底面,所以求圆柱侧面积即可。】
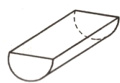
2. 一个半圆柱形木料,如图所示。已知它的底面直径是30厘米,长是10分米,它的表面积是多少?

答案:
30 厘米 = 3 分米 $\pi\times3\times10\div2 = 15\pi$(平方分米) $\pi\times(3\div2)^2 = 2.25\pi$(平方分米) $3\times10 = 30$(平方分米) $15\pi + 2.25\pi + 30=(17.25\pi + 30)$平方分米(或 84.165 平方分米)
3. 如图,用一张长为30.84分米的长方形铁皮正好可以做一个圆柱形油桶。这个油桶的表面积是多少?


答案:
$30.84\div(3.14 + 2)=6$(分米) $\pi\times(6\div2)^2 = 9\pi$(平方分米) $\pi\times6\times6 = 36\pi$(平方分米) $36\pi + 9\pi\times2 = 54\pi$(平方分米)(或 169.56 平方分米)【提示:观察发现,长方形的长 = 2 条直径 + 底面周长 = 直径×2 + $\pi$×直径 = ($\pi$ + 2)×直径,即 5.14 条直径是 30.84 分米,可求出直径,也就是做成的圆柱形水桶的高。】
4. 要做一个无盖的圆柱形水桶,有以下几种型号的铁皮可供选择。(π取3.14)

(1)选择( )号和( )号材料比较合适。
(2)做成的水桶的表面积是多少平方分米?

(1)选择( )号和( )号材料比较合适。
(2)做成的水桶的表面积是多少平方分米?
答案:
(1) ② ④
(2) $3.14\times(4\div2)^2 + 12.56\times5 = 75.36$(平方分米)
(1) ② ④
(2) $3.14\times(4\div2)^2 + 12.56\times5 = 75.36$(平方分米)
例 一个圆柱高10厘米,如果把高减少2厘米,所得到的新圆柱的表面积比原来减少12.56平方厘米。原来圆柱的表面积是多少平方厘米?
答案:
分析与解答 如图,高减少,底面积不变,减少的是侧面积,减少的侧面积 $=$ 底面周长×减少的高,算出底面周长,再算出底面半径,最后算出原来圆柱的表面积。
12.56÷2 $=$ 6.28(平方厘米)
6.28÷3.14÷2 $=$ 1(厘米)
π×1² $=$ $π($平方厘米)
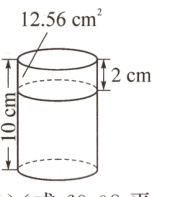
π×1×2×10 $=$ $20π($平方厘米)
π×2 $+$ 20π $=$ $22π($平方厘米$)($或69.08平方厘米)
小窍门 熟练掌握圆柱侧面积及表面积的计算方法,借助画图帮助分析,减少的表面积其实就是减少的那部分圆柱的侧面积。
分析与解答 如图,高减少,底面积不变,减少的是侧面积,减少的侧面积 $=$ 底面周长×减少的高,算出底面周长,再算出底面半径,最后算出原来圆柱的表面积。
12.56÷2 $=$ 6.28(平方厘米)
6.28÷3.14÷2 $=$ 1(厘米)
π×1² $=$ $π($平方厘米)

π×1×2×10 $=$ $20π($平方厘米)
π×2 $+$ 20π $=$ $22π($平方厘米$)($或69.08平方厘米)
小窍门 熟练掌握圆柱侧面积及表面积的计算方法,借助画图帮助分析,减少的表面积其实就是减少的那部分圆柱的侧面积。
1. 一个圆柱的底面周长和高相等,如果高增加2厘米,表面积就增加25.12平方厘米。原来这个圆柱的表面积是多少?(π取3.14)
答案:
$25.12\div2 = 12.56$(厘米) $12.56\div3.14\div2 = 2$(厘米) $3.14\times2^2\times2 + 12.56\times12.56 = 182.8736$(平方厘米)【提示:增加的面积 = 底面周长×2,可求出底面周长。】
2. 如图是一种双层生日蛋糕,每层的高度都是12厘米,上层的底面直径是20厘米,下层的底面直径是30厘米。在蛋糕表面抹一层奶油,抹奶油的面积是多少?


答案:
$\pi\times20\times12 + \pi\times30\times12 = 600\pi$(平方厘米) $\pi\times(30\div2)^2 = 225\pi$(平方厘米) $600\pi + 225\pi = 825\pi$(平方厘米)(或 2590.5 平方厘米)【提示:抹奶油的面积 = 大、小两个圆柱形蛋糕的侧面积 + 大圆柱形蛋糕的一个底面积。】
查看更多完整答案,请扫码查看


