《2025年核心素养天天练五年级数学下册北师大版》

1. 将一个长方体的高减少5 cm就变成了正方体，正方体的表面积比原来长方体的表面积减少了60 cm²。原长方体的体积是多少立方厘米？
　　思路分析 根据题意，可画图表示，由图可知，减少部分的面积实际就是阴影部分长方体的侧面积，也就是4个相等的长方形的面积。因为剩下的是一个正方体，所以4个长方形的长是相等的。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 60÷4÷5 = 3(cm)
3×3×(3 + 5) = 72(cm³)

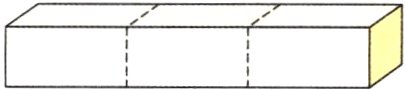
2. 一块长方体木料，长5 m，沿横截面把它截成3段，表面积增加24 dm²，原来这块长方体木料的体积是多少立方米？
　　　　

答案： 24÷4 = 6(dm²) 6 dm² = 0.06 m²
0.06×5 = 0.3(m²)
解析：由图可知，把这根长方体木料横截成3段，表面积增加了24 dm²，表面积增加的是4个截面的面积，据此可以求出一个截面的面积，再根据长方体的体积公式解答即可。

3. 三个形状相同的长方体铁块，长是8 cm，宽是6 cm，高是5 cm。把它们熔铸成一个大的长方体铁块，熔铸成的铁块长是18 cm，高是4 cm，它的宽是多少厘米?
　　思路分析 三个小长方体铁块熔铸成一个大长方体铁块，熔铸前后体积不变。

答案： 8×6×5×3÷(18×4) = 10(cm)

4. 一个封闭的长方体塑料盒，长12 cm，宽5 cm，高6 cm，里面的水高4 cm。现在把这个长方体竖起来，左侧面做底面，现在的水面高多少厘米？现在水和塑料盒的接触面积是多少平方厘米?

答案： 12×5×4÷(5×6) = 8(cm)
(8×6 + 8×5)×2 + 5×6 = 206(cm²)
解析：根据题意可知：平放和竖放塑料盒内的水的体积没变，只是水在塑料盒内的形状改变了。先根据长方体的体积公式求出塑料盒内水的体积，然后用体积除以竖放时容器的底面积，就是水面的高度；现在水与塑料盒的接触面积就是长6 cm、宽5 cm、高为此时水深的长方体5个面的面积(缺少上面)，根据长方体的表面积公式解答即可。

口算天天练 8.5 + 1.8 = 　9.2 - 5.4 = 　6.5×20 = 　4.5÷3 = 　6.8×0.5 = 　2.5×0.4 = 　1.5÷3 = 　2.8×5 = 　1.25×10 = 　0.8×1.5 = 　

答案： 10.3 3.8 130 1.5 3.4
1 0.5 14 12.5 1.2