《2025年课时练作业与测评九年级数学上册冀教版》

1. 用计算器求$\cos 15^{\circ}$，正确的按键顺序是( )

A.$\cos 15 =$
B.$\cos 15$
C.$Shift 15$
D.$15 \cos$

答案： 1.A

2. 用计算器求$\sin 62^{\circ}20'$的值约为(保留四位有效数字)( )

A.$0.8857$
B.$0.8856$
C.$0.8852$
D.$0.8851$

答案： 2.A

3. 计算$\sin 20^{\circ}-\cos 20^{\circ}$的值约为(保留四位有效数字)( )

A.$-0.5976$
B.$0.5976$
C.$-0.5977$
D.$0.5977$

答案： 3.C

4. 用计算器计算：$2\sin 15^{\circ}\cos 15^{\circ}=$______。

答案： 4.0.5

5. 在$Rt \triangle ABC$中，$\angle C = 90^{\circ}$，$a:b = 3:4$，运用计算器计算$\angle A$的度数(结果精确到$1^{\circ}$)约是( )

A.$30^{\circ}$
B.$37^{\circ}$
C.$38^{\circ}$
D.$39^{\circ}$

答案： 5.B

6. $\sin A = 0.2675$，则$\angle A \approx$______(结果精确到$0.1^{\circ}$)。

答案： 6.$15.5^{\circ}$

7. 已知$\sin \alpha = 0.2$，$\cos \beta = 0.8$，则$\alpha+\beta \approx$______(结果精确到$1'$)。

答案： 7.$48^{\circ}24'$

8. 下面四个数中，最大的是( )

A.$\sqrt{5}-\sqrt{3}$
B.$\sin 88^{\circ}$
C.$\tan 46^{\circ}$
D.$\frac{\sqrt{5}-1}{2}$

答案： 8.C

9. 已知：如图 26 - 2 - 1，在$\triangle ABC$中，$AB = 8$，$AC = 9$，$\angle A = 48^{\circ}$。
求：(1)$AB$边上的高(结果精确到$0.01$)。
(2)$\angle B$的度数(结果精确到$1'$)。

答案：
9.解：
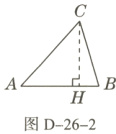
(1)如图 D-26-2,过点 $C$ 作 $AB$ 边上的高 $CH$，垂足为 $H$.
$\because$ 在 $Rt\triangle ACH$ 中, $\sin A = \frac{CH}{AC}$，
$\therefore CH = AC · \sin A = 9\sin 48^{\circ} \approx 6.69$.

(2)$\because$ 在 $Rt\triangle ACH$ 中, $\cos A = \frac{AH}{AC}$，
$\therefore AH = AC · \cos A = 9\cos 48^{\circ}$，
$\therefore$ 在 $Rt\triangle BCH$ 中,
$\tan B = \frac{CH}{BH} = \frac{CH}{AB - AH} = \frac{9\sin 48^{\circ}}{8 - 9\cos 48^{\circ}} \approx 3.382$，
$\therefore \angle B \approx 73^{\circ}32'$.

10. 数学归纳(1)验证下列两组数值的关系：
$2\sin 30^{\circ}\cos 30^{\circ}$与$\sin 60^{\circ}$；
$2\sin 22.5^{\circ}\cos 22.5^{\circ}$与$\sin 45^{\circ}$。
(2)用一句话概括上面的关系。
(3)试一试：你自己任选一个锐角，用计算器验证上述结论是否成立。
(4)如果结论成立，试用$\alpha$表示一个锐角，写出这个关系式。

答案： 10.解：
(1)$\because 2\sin 30^{\circ} \cos 30^{\circ} = 2 × \frac{1}{2} × \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2}$, $\sin 60^{\circ} = \frac{\sqrt{3}}{2}$, $2\sin 22.5^{\circ} \cos 22.5^{\circ} \approx 2 × 0.38 × 0.92 \approx 0.7$, $\sin 45^{\circ} = \frac{\sqrt{2}}{2} \approx 0.7$, $\therefore 2\sin 30^{\circ} \cos 30^{\circ} = \sin 60^{\circ}$, $2\sin 22.5^{\circ} \cos 22.5^{\circ} = \sin 45^{\circ}$.
(2)由
(1)可知,一个角的正弦与余弦积的 $2$ 倍等于该角 $2$ 倍的正弦值.
(3)$2\sin 15^{\circ} \cos 15^{\circ} = \frac{1}{2}$, $\sin 30^{\circ} = \frac{1}{2}$. 故结论成立.
(4)$2\sin \alpha \cos \alpha = \sin 2\alpha$.